
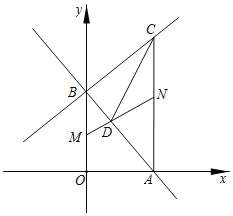
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y��kx+b��x�ύ�ڵ�A��5��0������y�ύ�ڵ�B��ֱ��y�T![]() x+6����B�͵�C����AC��x�ᣮ��M�ӵ�B������ÿ��2����λ���ȵ��ٶ���y�����O�˶���ͬʱ��N�ӵ�A������ÿ��3����λ���ȵ��ٶ�������AC���C�˶�������M�����Oʱ����M��Nͬʱֹͣ�˶������M�˶���ʱ��Ϊt���룩������MN��
x+6����B�͵�C����AC��x�ᣮ��M�ӵ�B������ÿ��2����λ���ȵ��ٶ���y�����O�˶���ͬʱ��N�ӵ�A������ÿ��3����λ���ȵ��ٶ�������AC���C�˶�������M�����Oʱ����M��Nͬʱֹͣ�˶������M�˶���ʱ��Ϊt���룩������MN��
��1����ֱ��y��kx+b�ĺ�������ʽ����C�����ꣻ
��2����MN��x��ʱ����t��ֵ��
��3��MN��AB���ڵ�D������CD���ڵ�M��N�˶������У��߶�CD�ij����Ƿ�仯������仯����ֱ��д���߶�CD���ȱ仯�ķ�Χ��������仯����ֱ��д���߶�CD�ij��ȣ�
���𰸡���1��y����![]() x+6����C������Ϊ��5��10������2��t��
x+6����C������Ϊ��5��10������2��t��![]() ����3���߶�CD�ij��Ȳ��仯��CD��
����3���߶�CD�ij��Ȳ��仯��CD��![]() �����ɼ�����
�����ɼ�����
��������
��1���������C�͵�B�����꣬�ٸ��ݴ���ϵ������������ô𰸣�
��2���ֱ��ú�t�Ĵ���ʽ��ʾOM��AN�ij����г�����t�ķ��̣�������⣻
��3������D��EF��x�ᣬ��OB��E����AC��F���ɡ�BDM�ס�ADN����![]() ���Ӷ���DF�ij����ɡ�BDE�ס�ADF����EO��FA��
���Ӷ���DF�ij����ɡ�BDE�ס�ADF����EO��FA��![]() ���Ӷ���CF�ij�������������⣮
���Ӷ���CF�ij�������������⣮
��1����AC��x�ᣬ��A��5��0����
���C�ĺ�����Ϊ5��
����y�T![]() x+6����x��5ʱ��y��
x+6����x��5ʱ��y��![]() ��5+6��10��
��5+6��10��
����x��0��y��6��
���C��������5��10������B��������0��6����
��ֱ��y��kx+b��x�ύ�ڵ�A��5��0������y�ύ�ڵ�B��0��6����
��![]() ����ã�
����ã�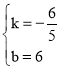 ��
��
��ֱ��y��kx+b�ĺ�������ʽΪ��y����![]() x+6��
x+6��
����������ֱ��y��kx+b�ĺ�������ʽΪy����![]() x+6����C������Ϊ��5��10����
x+6����C��������5��10����
��2��������ã�BM��2t��AN��3t��
��OM��6��2t��
�ߵ�OM��ANʱ��OM��AN��
���ı���EOAFΪƽ���ı��Σ�
��MN��x�ᣬ
��6��2t��3t��
��ã�t��![]() ��
��
�൱MN��x��ʱ��t��![]() ��
��
��3���߶�CD�ij��Ȳ��仯���������£�
����D��EF��x�ᣬ��OB��E����AC��F��
��EF��x�ᣬBM��AN����AOE��90����
���ı���EOAFΪ���Σ�
��EF��OA��5��EO��FA��
��BM��AN��
���BDM�ס�ADN��
��![]()
��EF��5��
��DE��2��DF��3��
��BM��AN��
���BDE�ס�ADF��
��![]() ��
��
��![]() ��
��
��OB��6��
��EO��FA��![]() ��
��
��CF��AC��FA��![]() ��
��
��CD��![]() ��
��![]() ��
��


 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д� ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
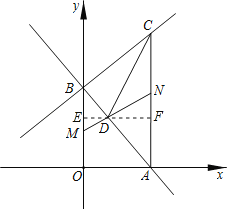
����Ŀ�����������Ǽס��ҡ������˸�10��Ͷ���ĵ÷֣�ÿ��Ͷ��10�Σ�ÿ��Ͷ�м�1�֣���
���÷ֵ�ƽ��������������7���÷�ͳ�Ʊ����£�
������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�÷� | 7 | 6 | 8 | a | 7 | 5 | 8 | b | 8 | 7 |
��1�����÷ֱ��е�a= ��b= ��
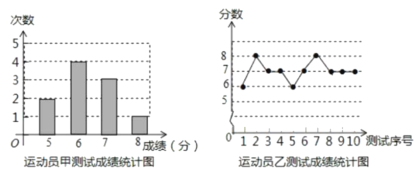
��2����������������ѡ��һλͶ���÷ָ��ҽ�Ϊ�ȶ���Ͷ����Ϊ����������Ϊѡ˭�����ʣ���������ѧ����ͳ��֪ʶ���Է���˵�����ο����ݣ�![]() ��
��![]() ��
��![]() ����
����
��3���ס��ҡ������˻���֮����д�����ϰ��ÿ���˵��ȿ��ܵĴ����������ˣ������ȴ������д������������δ�������ֻص������еĸ����Ƕ��٣�������״ͼ���б������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪԭ�㣬��B��x����������ϣ�D��0��8����������OBCD�۵���ʹ�ö���B����CD���ϵ�P�㴦.
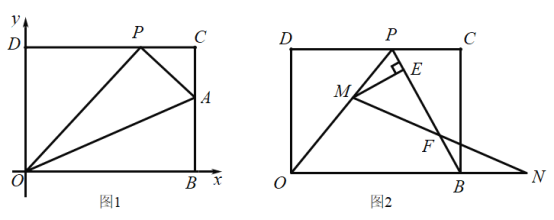
��1����ͼ1�еĵ� P ǡ����CD�ߵ��е㣬���AOB�Ķ���.
��2����ͼ1����֪�ۺ����BC���ڵ�A����OD=2CP�����A������.
��3����ͼ2���ڣ�2���������£���ȥ�ۺ�AO���߶�AP������BP������M���߶�OP�ϣ���M��P��O���غϣ�������N���߶�OB���ӳ����ϣ���BN=PM������MN��PB�ڵ�F����ME��BP�ڵ�E�����ʵ���M��N���ƶ������У��߶�EF�ij����Ƿ����仯��
���仯��˵�����ɣ������䣬����߶�EF�ij���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ͼ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ�![]() �ڷ���ֽ�е�λ����ͼ��ʾ��
�ڷ���ֽ�е�λ����ͼ��ʾ��

��1������ͼ�н���ƽ��ֱ������ϵ��ʹ��![]() ��
��![]() ���������ֱ�Ϊ
���������ֱ�Ϊ![]() ��
��![]() �����
����д��![]() ������ꣻ
������ꣻ
��2����ͼ������![]() ������ԭ����ת
������ԭ����ת![]() ���
���![]() �����
�����![]() ��
��![]() ��
��![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y������x��m��2��m+1��mΪ����������������������ǣ�������
A.��m��2ʱ�����������ֵ�ǩ�1
B.����ͼ��Ķ���ʼ����ֱ��y����x+1��ͼ����
C.����1��x��2ʱ��y��x�������������m��ȡֵ��ΧΪm��2
D.��m��0ʱ������ͼ��Ķ��㼰����ͼ����x����������㹹�ɵ��������ǵ���ֱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ͼ��λ��
��ͼ��λ��![]() ���·��IJ�����
���·��IJ�����![]() �ᷭ�������Ϸ������õ����º���
�ᷭ�������Ϸ������õ����º���![]() ��ͼ��.�����º���ͼ����ֱ��
��ͼ��.�����º���ͼ����ֱ��![]() ���������㣬��
���������㣬��![]() ��ȡֵ��ΧΪ___________��
��ȡֵ��ΧΪ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣�ʵʩ�¿γ̸ĸ��ѧ��������ѧϰ���������������кܴ���ߣ�����ʦΪ���˽����̰༶ѧ������ѧϰ�����������ľ���������Ա��ಿ��ѧ��������Ϊ�������µĸ��ٵ��飬�����������ֳ����࣬A���ر�ã�B���ã�C��һ�㣻D���ϲ�������������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺

��1�����ε����У�����ʦһ�������� ��ͬѧ������C��Ů���� ����D�������� ����
��2�������������ͳ��ͼ����������
��3��Ϊ�˹�ͬ����������ʦ��ӱ������A���D��ѧ���зֱ�ѡȡһλͬѧ���С�һ��һ������ѧϰ�������б���������ͼ�ķ��������ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������DE��ֱƽ�ְ뾶OA��CΪ���㣬��DF��뾶OB�ཻ�ڵ�P������EF��EO����DE��2����DPA��45�㣮
��1������O�İ뾶��
��2����ͼ����Ӱ���ֵ������
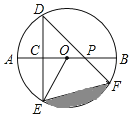
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() Ϊ���κ���
Ϊ���κ���![]() ͼ��Ķ��㣬ֱ��
ͼ��Ķ��㣬ֱ��![]() �ֱ�
�ֱ�![]() ��ĸ������
��ĸ������![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��
(1)�����κ���ͼ����![]() ������κ����Ľ���ʽ��
������κ����Ľ���ʽ��
(2)��ͼ������![]() ����Ϊ
����Ϊ![]() ���ҵ�
���ҵ�![]() ��
��![]() �ڲ�(�������߽�)��
�ڲ�(�������߽�)��
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ��
��![]() ���ڶ��κ���ͼ���ϣ��ԱȽ�
���ڶ��κ���ͼ���ϣ��ԱȽ�![]() ��
��![]() �Ĵ�С
�Ĵ�С

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com