
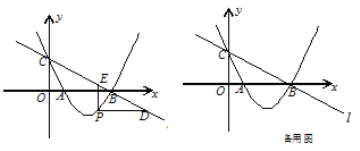
【题目】如图,直线![]() :
: ![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线![]() 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥![]() 轴交
轴交![]() 于点D,PE∥
于点D,PE∥![]() 轴交
轴交![]() 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线![]() 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
【答案】(1)抛物线的解析式为![]() (2)当
(2)当![]() 时,PD+PE的最大值是3(3)能,以A、B、P、F为顶点的四边形能构成平行四边形.此时点F的坐标为F(3,
时,PD+PE的最大值是3(3)能,以A、B、P、F为顶点的四边形能构成平行四边形.此时点F的坐标为F(3, ![]() )或F(1,
)或F(1, ![]() )
)
【解析】试题分析: (1)在![]() 中求出
中求出![]() 和
和![]() 时
时![]() 与
与![]() 的值可得点
的值可得点![]() 的坐标,根据点
的坐标,根据点![]() 坐标利用待定系数法可得抛物线解析式;
坐标利用待定系数法可得抛物线解析式;
(2)设P(![]() ,
, ![]() ),则D(
),则D(![]() ,
, ![]() ),
),
E(![]() ,
, ![]() ),用
),用![]() 表示出
表示出![]() ,配方即可求出最大值.
,配方即可求出最大值.
(3)令![]() ,求出点
,求出点![]() 坐标,求出
坐标,求出![]() 的值,然后分类讨论.
的值,然后分类讨论.
试题解析:
(1)∵直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,
轴分别交于点B、C,
∴B(2,0)、C(0,1),
∵B、C在抛物线解![]() 上,
上,
∴![]() ,
,
解得: 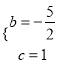 ,
,
∴抛物线的解析式为![]() .
.
(2)设P(![]() ,
, ![]() ),
),
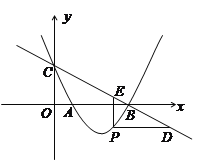
∵PD∥![]() 轴,PE∥
轴,PE∥![]() 轴,点D,E都在直线
轴,点D,E都在直线![]() 上,
上,
∴E(![]() ,
, ![]() ),D(
),D(![]() ,
, ![]() ),
),
∴PD+PE=![]() ,
,
![]() ,
,
![]() ,
,
∴当![]() 时,PD+PE的最大值是3.
时,PD+PE的最大值是3.
(3)能,理由如下:
由![]() ,令
,令![]() ,
,
解得: ![]() ,
, ![]() ,
,
∴A(![]() ,0),B(2,0),
,0),B(2,0),
∴![]() ,
,
若以A、B、P、F为顶点的四边形能构成平行四边形,
①当以AB为边时,则AB∥PF且AB=PF,
设P(![]() ,
, ![]() ),则F(
),则F(![]() ,
, ![]() ),
),
∴![]() ,
,
整理得: ![]() ,
,
解得: ![]() ,
, ![]() (与A重合,舍去),
(与A重合,舍去),
∴F(3, ![]() ),
),
②当以AB为对角线时,连接PF交AB于点G,则AG=BG,PG=FG,
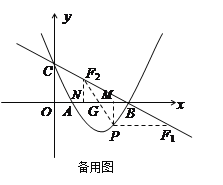
设G(m,0),
∵A(![]() ,0),B(2,0),
,0),B(2,0),
∴m-![]() =2-m,∴m=
=2-m,∴m=![]() ,
,
∴G(![]() ,0),
,0),
作PM⊥AB于点M,FN⊥AB于点N,则NG=MG,PM=FN,
设P(![]() ,
, ![]() ),则F(
),则F(![]() ,
, ![]() ),
),
∴![]() ,
,
整理得: ![]() ,
,
解得: ![]() ,
, ![]() (与A重合,舍去),
(与A重合,舍去),
∴F(1, ![]() ).
).
综上所述,以A、B、P、F为顶点的四边形能构成平行四边形.此时点F的坐标为F(3, ![]() )或F(1,
)或F(1, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】为了了解学校图书馆上个月借阅情况,管理老师从学生对艺术、经济、科普及生活四类图书借阅情况进行了统计,并绘制了下列不完整的统计图,请根据图中信息解答下列问题:
(1)上个月借阅图书的学生有多少人?扇形统计图中“艺术”部分的圆心角度数是多少?
(2)把条形统计图补充完整;
(3)从借阅情况分析,如果要添置这四类图书300册,请你估算“科普”类图书应添置多少册合适?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,过点
的中点,过点![]() 的直线分别与
的直线分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .若
.若![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 是菱形;④
是菱形;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A为平面直角坐标系第一象限内一点,直线y=x过点A,过点A作AD⊥y轴于点D,点B是y轴正半轴上一动点,连接AB,过点A作AC⊥AB交x轴于点C.
(1)如图,当点B在线段OD上时,求证:AB=AC;
(2)①如图,当点B在OD延长线上,且点C在x轴正半轴上, OA、OB、OC之间的数量关系为________(不用说明理由);
②当点B在OD延长线上,且点C在x轴负半轴上,写出OA、OB、OC之间的数量关系,并说明原因.
(3)直线BC分别与直线AD、直线y=x交于点E、F,若BE=5,CF=12,直接写出AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一枚质地均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这枚骰子掷出后,求:

(1)“6”朝上的概率是多少?
(2)哪个数字朝上的概率最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新型冠状病毒肺炎疫情肆虐,红星社区为了提高社区居民的身体素质,鼓励居民在家锻炼,特采购了一批跳绳免费发放,已知2根幸福牌跳绳和1根平安牌跳绳共需31元,2根平安牌跳绳和3根幸福牌跳绳共需54元.
(1)求幸福牌跳绳和平安牌跳绳的单价;
(2)已知该社区需要采购两种品牌的跳绳共60根,且平安牌跳绳的数量不少于幸福牌跳绳数量的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
(1)求证:AC是⊙O的切线;
(2)若sinC=![]() ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com