
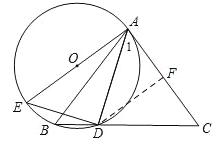
【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
(1)求证:AC是⊙O的切线;
(2)若sinC=![]() ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.

【答案】(1)详见解析;(2)⊙O的直径为![]() .
.
【解析】试题分析:(1)根据等腰三角形的性质,由AB=AC,AD=DC得∠C=∠B,∠1=∠C,则∠1=∠B,根据圆周角定理得∠E=∠B,∠ADE=90°,所以∠1+∠EAD=90°,然后根据切线的判定定理即可得到AC是⊙O的切线;
(2)过点D作DF⊥AC于点F,如图,根据等腰三角形的性质得CF=![]() AC=3,在Rt△CDF中,利用正弦定义得sinC=
AC=3,在Rt△CDF中,利用正弦定义得sinC=![]() =
=![]() ,则设DF=4x,DC=5x,利用勾股定理得CF=3x,所以3x=3,解得x=1,于是得到DC=AD=5,然后证明△ADE∽△DFC,再利用相似比可计算AE即可.
,则设DF=4x,DC=5x,利用勾股定理得CF=3x,所以3x=3,解得x=1,于是得到DC=AD=5,然后证明△ADE∽△DFC,再利用相似比可计算AE即可.
试题解析:(1)∵AB=AC,AD=DC,
∴∠C=∠B,∠1=∠C,
∴∠1=∠B,
又∵∠E=∠B,
∴∠1=∠E,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠EAD=90°,
∴∠1+∠EAD=90°,即∠EAC=90°,
∴AE⊥AC,
∴AC是⊙O的切线;
(2)过点D作DF⊥AC于点F,如图,
∵DA=DC,
∴CF=![]() AC=3,
AC=3,
在Rt△CDF中,∵sinC=![]() =
=![]() ,
,
设DF=4x,DC=5x,
∴CF=![]() =3x,
=3x,
∴3x=3,解得x=1,
∴DC=5,
∴AD=5,
∵∠ADE=∠DFC=90°,∠E=∠C,
∴△ADE∽△DFC,
∴![]() ,即
,即![]() ,解得AE=
,解得AE=![]() ,
,
即⊙O的直径为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如右:甲:8,7,10,7,8; 乙:9,5,10,9,7.
(1)将下表填写完整:
平 均 数 | 方 差 | |
甲 | ||
乙 | 3.2 |
(2)若你是教练,根据以上信息,你会选择谁参加射击比赛,理由是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 两个互为相反数的和是0; B. 两个互为相反数的绝对值相等;
C. 两个互为相反数的商是-1; D. 两个互为相反数的平方相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一列式子,按一定规律排列成﹣3a2 , 9a5 , ﹣27a10 , 81a17 , ﹣243a26 , ….
(1)当a=1时,其中三个相邻数的和是63,则位于这三个数中间的数是
(2)上列式子中第n个式子为(n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的表示集合的大括号内: ![]() ,﹣0.
,﹣0. ![]() ,﹣(﹣2),﹣
,﹣(﹣2),﹣ ![]() ,1.732,
,1.732, ![]() ,0,
,0, ![]() ,1.1010010001…(每两个1之间依次多一个0) 整 数{…}
,1.1010010001…(每两个1之间依次多一个0) 整 数{…}
正分数{…}
无理数{…}
实 数 {…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
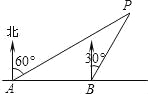
【题目】如图,李明同学在东西方向的滨海路A处,测得海中灯塔P在北偏东60°方向上,他向东走400米至B处,测得灯塔P在北偏东30°方向上,求灯塔P到滨海路的距离.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com