
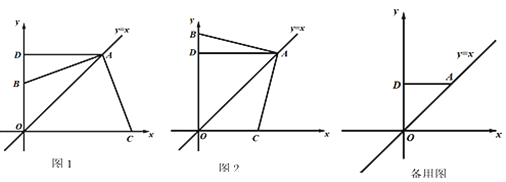
【题目】如图,点A为平面直角坐标系第一象限内一点,直线y=x过点A,过点A作AD⊥y轴于点D,点B是y轴正半轴上一动点,连接AB,过点A作AC⊥AB交x轴于点C.
(1)如图,当点B在线段OD上时,求证:AB=AC;
(2)①如图,当点B在OD延长线上,且点C在x轴正半轴上, OA、OB、OC之间的数量关系为________(不用说明理由);
②当点B在OD延长线上,且点C在x轴负半轴上,写出OA、OB、OC之间的数量关系,并说明原因.
(3)直线BC分别与直线AD、直线y=x交于点E、F,若BE=5,CF=12,直接写出AB的长.
【答案】(1)证明见解析;(2)①OA=![]() (OC+OB);②OA=
(OC+OB);②OA=![]() (OB-OC);(3)10
(OB-OC);(3)10![]() ; 15
; 15![]() .
.
【解析】
(1)过点A作AE⊥OC于点E,先证明四边形ADOE是正方形,再证明Rt△ADB≌Rt△AEC(AAS),从而求得结论;(2)①过点A作AE⊥OC于点E,方法同(1)证明四边形ADOE是正方形,Rt△ADB≌Rt△AEC,△AOD是等腰直角三角形,再应用勾股定理即可得结论OA=![]() (OC+OB);②方法同①得结论:OA=
(OC+OB);②方法同①得结论:OA=![]() (OB-OC);(3)①当点B在线段OD上时,将△AFC绕点A顺时针旋转90°,AC与AB重合,变为△ABF′,连接EF′,证明∠EBF′=90°,由勾股定理得EF′=13,再证明△AEF≌△AEF′,所以EF= EF′=13,BF=EF-EB=13-5=8,BC=BF+FC=8+12=20,而△ABC是等腰直角三角形,所以AB=
(OB-OC);(3)①当点B在线段OD上时,将△AFC绕点A顺时针旋转90°,AC与AB重合,变为△ABF′,连接EF′,证明∠EBF′=90°,由勾股定理得EF′=13,再证明△AEF≌△AEF′,所以EF= EF′=13,BF=EF-EB=13-5=8,BC=BF+FC=8+12=20,而△ABC是等腰直角三角形,所以AB=![]() =10
=10![]() ; ②当点B在OD延长线上,且点C在x轴正半轴上时,方法同①,解得:AB=15
; ②当点B在OD延长线上,且点C在x轴正半轴上时,方法同①,解得:AB=15![]() ;③当点B在OD延长线上,且点C在x轴负半轴上时,方法同上,解得:AB=3
;③当点B在OD延长线上,且点C在x轴负半轴上时,方法同上,解得:AB=3![]() .
.
(1)过点A作AE⊥OC于点E,
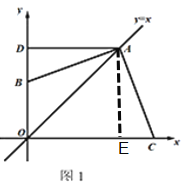
∵AD⊥y,点A在y=x上,∠DOE=90°
∴四边形ADOE是矩形,AE=OE,
∴矩形ADOE是正方形,
∴AD=AE,∠DAE=∠BAC=90°,
∴∠DAB=∠EAC,
又∵∠BDA=∠CEA=90°
∴Rt△ADB≌Rt△AEC
∴AB=AC.
(2)① 过点A作AE⊥OC于点E,
方法同(1)得,四边形ADOE是正方形,Rt△ADB≌Rt△AEC,AB=AC,BD=CE,
∴OC+OB=OC+OD+BD=OC+OD+CE=OE+OD=2OD,即OD=![]() (OC+OB)
(OC+OB)
又∵△AOD是等腰直角三角形,
∴由勾股定理得:OA=![]() OD =
OD =![]() ×
×![]() (OC+OB)=
(OC+OB)=![]() (OC+OB),
(OC+OB),
即OA=![]() (OC+OB),
(OC+OB),
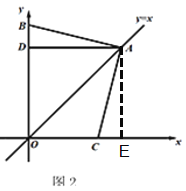
②过点A作AE⊥OC于点E,
方法同(1)得,四边形ADOE是正方形,Rt△ADB≌Rt△AEC,AB=AC,BD=CE,
∴OB-OD=OC+OE,即OB-OC=OD+OE=2OD=![]() OA,
OA,
又∵△AOD是等腰直角三角形,
∴由勾股定理得:OA=![]() OD,OD=
OD,OD= ![]() OA ,
OA ,
∴OB-OC= OD+OE=2OD=![]() OA,即OB-OC=
OA,即OB-OC=![]() OA,OA=
OA,OA=![]() (OB-OC)
(OB-OC)
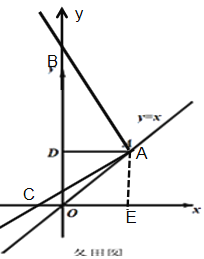
(3)①当点B在线段OD上时,
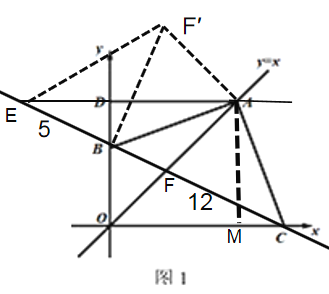
将△AFC绕点A顺时针旋转90°,AC与AB重合,变为△ABF′,连接EF′,BF′=CF=12,∠ACB=∠ABC=∠ABF′=45°,∠CBF′=∠ABC+∠ABF′=90°,所以∠EBF′=90°,
又∵BE=5,∴EF′=13,
∵∠F′AO=90°, ∠FAE=∠F′AE=45°,AE=AE,AF=AF′,
∴△AEF≌△AEF′
∴EF= EF′=13,BF=EF-EB=13-5=8,BC=BF+FC=8+12=20,
由(1)得:△ABC是等腰直角三角形,∴AB=![]() =10
=10![]() ;
;
②当点B在OD延长线上,且点C在x轴正半轴上时,
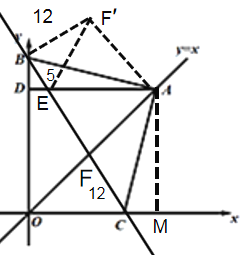
方法同①,旋转△AFC到△AF′B,证出∠EBF′,EF′=13=EF,BC=BE+EF+FC=5+13+12=30,所以等腰直角三角形ABC的直角边AB=15![]() ;
;
③当点B在OD延长线上,且点C在x轴负半轴上,

已证△ABC是等腰直角三角形,
过点B作BF′⊥BC于点B,截取 BF′=CF=12, 连接F′E、F′A,∵BE=5,
∴∠ABF′=∠ACF=135°,EF′=13
AB=AC,
∴△ABF′≌△ACF,可得AF′=AF,∠BAF′=∠CAF,
∴∠BAC=∠F′AF=90°,
∵∠EAF=45°,
∴∠EAF=45°=∠EAF′,又AE=AE
∴△EAF≌△EAF′,
∴EF=EF′=13,EC=EF-CF=13-12=1,BC=BE+EC=1+5=6,
∴在等腰直角三角形ABC中,直角边AB=3![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】某商场正在销售![]() 、
、![]() 两种型号玩具,已知购买一个
两种型号玩具,已知购买一个![]() 型玩具和两个
型玩具和两个![]() 型玩具共需
型玩具共需![]() 元;购买两个
元;购买两个![]() 型玩具和一个
型玩具和一个![]() 型玩具共需
型玩具共需![]() 元.
元.
(1)求一个![]() 型玩具和一个
型玩具和一个![]() 型玩具的价格各是多少元?
型玩具的价格各是多少元?
(2)我公司准备购买这两种型号的玩具共![]() 个送给幼儿园,且购买金额不能超过
个送给幼儿园,且购买金额不能超过![]() 元,请你帮该公司设计购买方案?
元,请你帮该公司设计购买方案?
(3)在(2)的前提下,若要求![]() 、
、![]() 两种型号玩具都要购买,且费用最少,请你选择一种最佳的设计方案,并通过计算说明。
两种型号玩具都要购买,且费用最少,请你选择一种最佳的设计方案,并通过计算说明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(![]() 分)在菱形
分)在菱形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点.
上的一个动点.
(![]() )如图①,求
)如图①,求![]() 的最小值.
的最小值.
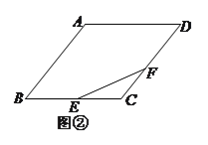
(![]() )如图②,若
)如图②,若![]() 也是
也是![]() 边上的一个动点,且
边上的一个动点,且![]() ,求
,求![]() 的最小值.
的最小值.
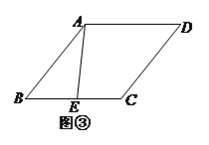
(![]() )如图③,若
)如图③,若![]() ,则在菱形内部存在一点
,则在菱形内部存在一点![]() ,使得点
,使得点![]() 分别到点
分别到点![]() 、点
、点![]() 、边
、边![]() 的距离之和最小.请你画出这样的点
的距离之和最小.请你画出这样的点![]() ,并求出这个最小值.
,并求出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个长方形的边长如图所示(![]() 为正整数),其面积分别为
为正整数),其面积分别为![]() .
.
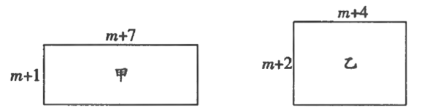
(1)填空:![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)若一个正方形的周长等于甲、乙两个长方形的周长之和.
①设该正方形的边长为![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示);
的代数式表示);
②设该正方形的面积为![]() ,试探究:
,试探究: ![]() 与
与![]() 的差是否是常数?若是常数,求出这个常数,若不是常数,请说明理由,
的差是否是常数?若是常数,求出这个常数,若不是常数,请说明理由,
(3)若另一个正方形的边长为正整数![]() ,并且满足条件
,并且满足条件![]() 的
的![]() 有且只有4个,求
有且只有4个,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB=AC=8,BO=![]() AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.
AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
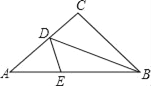
【题目】如图,三角形纸牌中,AB=8cm,BC=6cm,AC=5cm,沿着过△ABC的顶点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED周长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
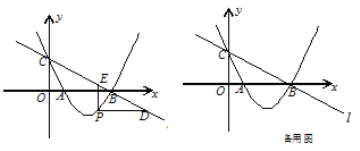
【题目】如图,直线![]() :
: ![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线![]() 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥![]() 轴交
轴交![]() 于点D,PE∥
于点D,PE∥![]() 轴交
轴交![]() 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线![]() 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com