
【题目】如图,Rt△ABC中,AB=AC=8,BO=![]() AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.
AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.

【答案】8+4![]() .
.
【解析】
过点O作OB′⊥AB于点O,交BC于点B′,连接B′N并延长交AB于点E,易证△BOM≌△B′ON(SAS),∴点N始终在经过点B′且与BC垂直的射线上,因为△CAN周长=CA+AN+CN=8+ AN+CN,所以AN+CN值最小时,周长最小,属于最短路径问题,关键找点C关于B′E的对称点C′,连接A C′,与B′E的交点N′即为周长最小时的点N,此时AN+CN=AC′,求出AC′的值即可求出周长最小值.
解:过点O作OB′⊥AB于点O,交BC于点B′,连接B′N并延长交AB于点E,∵Rt△ABC中,AB=AC,
∴∠OBB′=45°=∠OB′B,OB =OB′
又∵∠BOB′=∠MON=90°
∴∠BOM=∠B′ON
∴△BOM≌△B′ON(SAS)
∴∠OBB′=45°=∠OB′N,即∠BB′N=90°,OB′= OB=2,BB′=2![]() ,
,
∴点N始终在经过点B′且与BC垂直的射线上,
易证△BB′E是等腰直角三角形,BE=4,即BE=AE,
∵△CAN周长=CA+AN+CN=8+ AN+CN
∴AN+CN值最小时,周长最小,属于最短路径问题,
∴找点C关于B′E的对称点C′,连接A C′,与B′E的交点N′即为周长最小时的点N,此时AN+CN=AC′,
等腰直角三角形△BB′E中, 由勾股定理得BB′=2![]() ,
,
等腰直角三角形△ABC中, BC=8![]() 由三线合一得:BD=DC=AD=
由三线合一得:BD=DC=AD=![]() BC=4
BC=4![]() ,
,
∴B′C=BC- BB′=8![]() -2
-2![]() =6
=6![]() ,由对称性得:B′C=B′C′=6
,由对称性得:B′C=B′C′=6![]() ,
,
∴C′D=12![]() -4
-4![]() =8
=8![]() ,
,
即:Rt△AC′D中,A C′=![]() =
=![]() =4
=4![]()
∴△CAN周长的最小值=8+ AN+CN=8+4![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
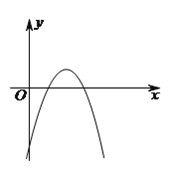
【题目】(![]() 分)如图,抛物线
分)如图,抛物线![]() 的顶点为
的顶点为![]() .
.
(![]() )求抛物线
)求抛物线![]() 的函数表达式.
的函数表达式.
(![]() )若抛物线形
)若抛物线形![]() 与
与![]() 关于
关于![]() 轴对称,求抛物线
轴对称,求抛物线![]() 的函数表达式.
的函数表达式.
(![]() )在(
)在(![]() )的基础上,设
)的基础上,设![]() 上的点
上的点![]() 、
、![]() 始终与
始终与![]() 上的点
上的点![]() 、
、![]() 分别关于
分别关于![]() 轴对称,是否存在点
轴对称,是否存在点![]() 、
、![]() (
(![]() 、
、![]() 分别位于抛物线对称轴两侧,且
分别位于抛物线对称轴两侧,且![]() 在
在![]() 的左侧),使四边形
的左侧),使四边形![]() 为正方形?
为正方形?
若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,过点
的中点,过点![]() 的直线分别与
的直线分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .若
.若![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 是菱形;④
是菱形;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是菱形,以点
是菱形,以点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴建立平面直角坐标系.若点
轴建立平面直角坐标系.若点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() .
.
(1)求菱形![]() 的边长;
的边长;
(2)证明![]() 为直角三角形;
为直角三角形;
(3)直线![]() 上是否存在一点
上是否存在一点![]() 使得
使得![]() 的面积与
的面积与![]() 的面积相等?若存在,请求出点
的面积相等?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
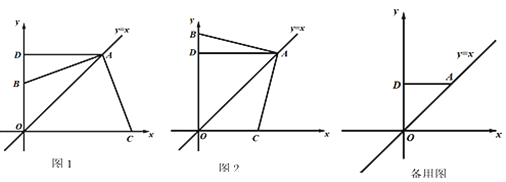
【题目】如图,点A为平面直角坐标系第一象限内一点,直线y=x过点A,过点A作AD⊥y轴于点D,点B是y轴正半轴上一动点,连接AB,过点A作AC⊥AB交x轴于点C.
(1)如图,当点B在线段OD上时,求证:AB=AC;
(2)①如图,当点B在OD延长线上,且点C在x轴正半轴上, OA、OB、OC之间的数量关系为________(不用说明理由);
②当点B在OD延长线上,且点C在x轴负半轴上,写出OA、OB、OC之间的数量关系,并说明原因.
(3)直线BC分别与直线AD、直线y=x交于点E、F,若BE=5,CF=12,直接写出AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一枚质地均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这枚骰子掷出后,求:

(1)“6”朝上的概率是多少?
(2)哪个数字朝上的概率最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中正确的个数为( )
①AB与AC互相垂直;
②AD与AC互相垂直;
③点C到AB的垂线段是线段AB;
④线段AB的长度是点B到AC的距离;
⑤线段AB是B点到AC的距离.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com