
【题目】(![]() 分)如图,抛物线
分)如图,抛物线![]() 的顶点为
的顶点为![]() .
.
(![]() )求抛物线
)求抛物线![]() 的函数表达式.
的函数表达式.
(![]() )若抛物线形
)若抛物线形![]() 与
与![]() 关于
关于![]() 轴对称,求抛物线
轴对称,求抛物线![]() 的函数表达式.
的函数表达式.
(![]() )在(
)在(![]() )的基础上,设
)的基础上,设![]() 上的点
上的点![]() 、
、![]() 始终与
始终与![]() 上的点
上的点![]() 、
、![]() 分别关于
分别关于![]() 轴对称,是否存在点
轴对称,是否存在点![]() 、
、![]() (
(![]() 、
、![]() 分别位于抛物线对称轴两侧,且
分别位于抛物线对称轴两侧,且![]() 在
在![]() 的左侧),使四边形
的左侧),使四边形![]() 为正方形?
为正方形?
若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
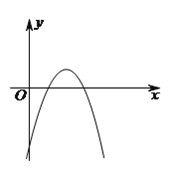
【答案】(1)y=-x2+6x-7;(2)y=x2-6x+7;(3)存在,(2,1)或(1,-2)
【解析】试题分析: ![]() 根据顶点坐标,求出
根据顶点坐标,求出![]() 的值,求抛物线
的值,求抛物线![]() 的函数表达式.
的函数表达式.
![]() 抛物线
抛物线![]() 与
与![]() 关于
关于![]() 轴对称,求出抛物线
轴对称,求出抛物线![]() 的顶点坐标和二次项系数,即可求得函数表达式.
的顶点坐标和二次项系数,即可求得函数表达式.
![]() 根据正方形的边长相等,
根据正方形的边长相等, ![]() .列出方程,求解即可.
.列出方程,求解即可.
试题解析:
(![]() )抛物线
)抛物线![]() 的顶点为
的顶点为![]() .
.
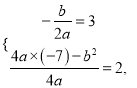
解得: ![]()
![]() .
.
(![]() )若抛物线
)若抛物线![]() 的顶点坐标为
的顶点坐标为![]() .
. ![]()
若抛物线![]() 与
与![]() 关于
关于![]() 轴对称,
轴对称,
抛物线![]() 的顶点坐标为:
的顶点坐标为: ![]()
![]()
抛物线![]() 的函数表达式为:
的函数表达式为:
![]() .
.
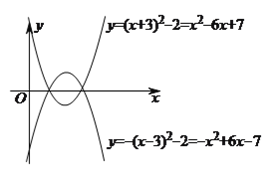
(![]() )存在.
)存在.
如图,要使四边形![]() 是正方形,
是正方形,
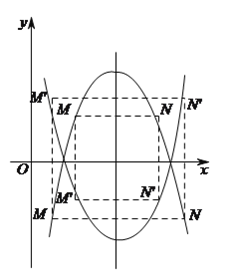
∵![]() 轴,则要
轴,则要![]() 轴,
轴,
且![]() .
.
设![]() ,
, ![]() ,
,
∵抛物线的对称轴为:直线![]() ,
,
∴由抛物线的对称性可知![]() ,
,
∴![]() .
.
当![]() ,
,
解得: ![]() ,(
,( ![]() 舍去),此时
舍去),此时![]() ,
,
当![]() 时,
时, ![]() ,
,
解得: ![]() ,(
,( ![]() 舍去),此时
舍去),此时![]() ,
,
综上,存在这样的点![]() 或
或![]() .
.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,EF//AB,GH//BC,EF、GH的交点P在BD上,图中面积相等的矩形有( )

A.1对B.2对C.3对D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢球后,足球踢到了小华处的概率是多少(用树状图或列表的方法加以说明)?
(2)如果踢三次后,球踢到了小明处的可能性最小,应从谁开始踢?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分![]() 分)小明、小华在一栋高楼前感慨楼房真高.小明说:“这楼起码
分)小明、小华在一栋高楼前感慨楼房真高.小明说:“这楼起码![]() 层!”小华却不以为然:“
层!”小华却不以为然:“![]() 层?我看没有!”小明说:“有本事,就让我们一起来测量吧!”
层?我看没有!”小明说:“有本事,就让我们一起来测量吧!”
如图,矩形![]() 表示楼体,小明、小华在楼体两侧各选
表示楼体,小明、小华在楼体两侧各选![]() 、
、![]() 两点,使得
两点,使得![]() 、
、![]() 、
、![]() 、
、![]() 四点在同一直线上,利用皮尺和侧倾器测得如下数据,
四点在同一直线上,利用皮尺和侧倾器测得如下数据, ![]() 米,
米, ![]() 米,
米, ![]() ,
, ![]() .
.
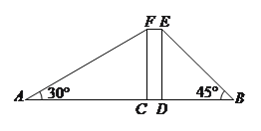
(![]() )请你帮助他们算一算楼高.(结果保留根号)
)请你帮助他们算一算楼高.(结果保留根号)
(![]() )若每层楼按
)若每层楼按![]() 米计算,你支持小明还是小华的观点呢?请说明理由.
米计算,你支持小明还是小华的观点呢?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(![]() 分)在菱形
分)在菱形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点.
上的一个动点.
(![]() )如图①,求
)如图①,求![]() 的最小值.
的最小值.
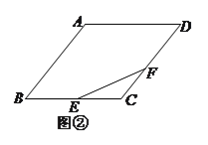
(![]() )如图②,若
)如图②,若![]() 也是
也是![]() 边上的一个动点,且
边上的一个动点,且![]() ,求
,求![]() 的最小值.
的最小值.
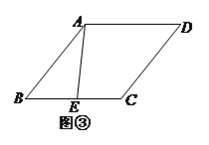
(![]() )如图③,若
)如图③,若![]() ,则在菱形内部存在一点
,则在菱形内部存在一点![]() ,使得点
,使得点![]() 分别到点
分别到点![]() 、点
、点![]() 、边
、边![]() 的距离之和最小.请你画出这样的点
的距离之和最小.请你画出这样的点![]() ,并求出这个最小值.
,并求出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB=AC=8,BO=![]() AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.
AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
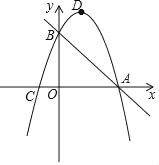
【题目】已知,如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)若点M为抛物线上一动点,是否存在点M,使△ACM与△ABC的面积相等?若存在,求点M的坐标;若不存在,请说明理由.
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,确定点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com