
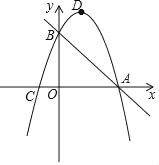
【题目】已知,如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)若点M为抛物线上一动点,是否存在点M,使△ACM与△ABC的面积相等?若存在,求点M的坐标;若不存在,请说明理由.
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,确定点N的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)点M的坐标为(0、3)或2,3)或(1+![]() ,﹣3)或(1﹣
,﹣3)或(1﹣![]() ,﹣3);(3)点N的坐标为(1,0)或(﹣7,0).
,﹣3);(3)点N的坐标为(1,0)或(﹣7,0).
【解析】试题分析:(1)先求得点A和点B的坐标,然后将点A和点B的坐标代入抛物线的解析式求得b,c的值即可;
(2)设M的坐标为(x,y),由△ACM与△ABC的面积相等可得到|y|=3,将y=3或y=-3代入抛物线的解析式求得对应的x的值,从而得到点M的坐标;
(3)先利用配方法求得点D的坐标,当∠DNA=90°时,DN⊥OA,可得到点N的坐标,从而得到AN=2,然后再求得AD的长;当∠N′DA=90°时,依据sin∠DN′A=sin∠ADN可求得AN′的长,从而可得到N′的解析式.
试题解析:(1)将x=0代入AB的解析式得:y=3,
∴B(0,3).
将y=0代入AB的解析式得:﹣x+3=0,解得x=3,
A(3,0).
将点A和点B的坐标代入得: ![]() ,
,
解得:b=2,c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)设M的坐标为(x,y).
∵△ACM与△ABC的面积相等,
∴![]() AC|y|=
AC|y|=![]() ACOB.
ACOB.
∴|y|=OB=3.
当y=3时,﹣x2+2x+3=3,解得x=0或x=2,
∴M(2,3)、(0、3).
当y=﹣3时,﹣x2+2x+3=3,解得:x=1+![]() 或x=1﹣
或x=1﹣![]() .
.
∴M(1+![]() ,﹣3)或(1﹣
,﹣3)或(1﹣![]() ,﹣3).
,﹣3).
综上所述点M的坐标为(0、3)或2,3)或(1+![]() ,﹣3)或(1﹣
,﹣3)或(1﹣![]() ,﹣3).
,﹣3).
(3)y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
①当∠DNA=90°时,如图所示:
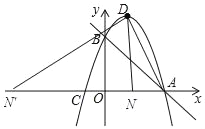
∵∠DNA=90°时,
∴DN⊥OA.
又∵D(1,4)
∴N(1,0).
∴AN=2.
∵DN=4,AN=2,
∴AD=2![]() .
.
②当∠N′DA=90°时,则DN′A=∠NDA.
∴![]() ,即
,即![]() ,解得:AN′=10.
,解得:AN′=10.
∵A(3,0),
∴N′(﹣7,0).
综上所述点N的坐标为(1,0)或(﹣7,0).


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
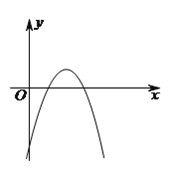
【题目】(![]() 分)如图,抛物线
分)如图,抛物线![]() 的顶点为
的顶点为![]() .
.
(![]() )求抛物线
)求抛物线![]() 的函数表达式.
的函数表达式.
(![]() )若抛物线形
)若抛物线形![]() 与
与![]() 关于
关于![]() 轴对称,求抛物线
轴对称,求抛物线![]() 的函数表达式.
的函数表达式.
(![]() )在(
)在(![]() )的基础上,设
)的基础上,设![]() 上的点
上的点![]() 、
、![]() 始终与
始终与![]() 上的点
上的点![]() 、
、![]() 分别关于
分别关于![]() 轴对称,是否存在点
轴对称,是否存在点![]() 、
、![]() (
(![]() 、
、![]() 分别位于抛物线对称轴两侧,且
分别位于抛物线对称轴两侧,且![]() 在
在![]() 的左侧),使四边形
的左侧),使四边形![]() 为正方形?
为正方形?
若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一枚质地均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这枚骰子掷出后,求:

(1)“6”朝上的概率是多少?
(2)哪个数字朝上的概率最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某百货商店服装柜在销售中发现:某品牌童装每天可售出20件,每件盈利40元,经市场调查发现,在进货价不变的情况下,若每件童装每降价1元,日销售量将增加2件.
(1)当每件童装降价多少元时,一天的盈利最多?
(2)若商场要求一天的盈利为1200元,同时又使顾客得到实惠,每件童装降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数图象经过(﹣2,4).
(1)如果点(a,1)和(﹣1,b)在函数图象上,求a,b的值;
(2)过图象上一点P作y轴的垂线,垂足为Q,S△OPQ=![]() ,求Q的坐标.
,求Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AD⊥BC,垂足为D,则下面的结论中正确的个数为( )
①AB与AC互相垂直;
②AD与AC互相垂直;
③点C到AB的垂线段是线段AB;
④线段AB的长度是点B到AC的距离;
⑤线段AB是B点到AC的距离.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com