
【题目】如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为________.

【答案】50
【解析】
易证△AEO≌△BAH,△BCH≌△CDF即可求得AO=BH,AH=EO,CH=DF,BH=CF,即可求得梯形DEOF的面积和△AEO,△ABH,△CGH,△CDF的面积,即可解题.
∵∠EAO+∠BAH=90°,∠EAO+∠AEO=90°,
∴∠BAH=∠AEO,
∵在△AEO和△BAH中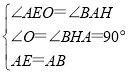 ,
,
∴△AEO≌△BAH(AAS),
同理△BCH≌△CDF(AAS),
∴AO=BG=3,AH=EO=6,CH=DF=4,BH=CF=3,
∵梯形DEOF的面积=![]() (EF+DH)FH=80,
(EF+DH)FH=80,
S△AEO=S△ABH=![]() AFAE=9,
AFAE=9,
S△BCH=S△CDF=![]() CHDH=6,
CHDH=6,
∴图中实线所围成的图形的面积S=80-2×9-2×6=50,
故选:B.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
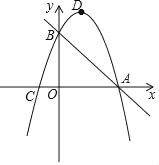
【题目】已知,如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)若点M为抛物线上一动点,是否存在点M,使△ACM与△ABC的面积相等?若存在,求点M的坐标;若不存在,请说明理由.
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,确定点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A,B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表所示,
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)在这三次购物中,第 次购物打了折扣;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
查看答案和解析>>
科目:初中数学 来源: 题型:
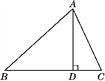
【题目】如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sin C=![]() ,BC=12,求△ABC的面积.
,BC=12,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
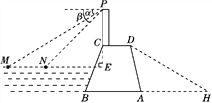
【题目】某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米).
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1∶0.25.为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方进行加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度i=1∶1.75.施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备.工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据:tan 31°≈0.60,sin 31°≈0.52)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0).下列结论:①ab<0;②b2>4a;③0<a+b+c<2;④0<b<1;⑤当x>-1时,y>0.其中正确结论的个数是( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“汉字听写”比赛,全体学生都参与,每名学生听写39个汉字,比赛结束后,学校随机抽查了部分学生的听写结果,绘制成如下所示的统计表(不完整)和如图所示的统计图(不完整) .请根据题意解答下列问题.
组别 | 正确的个数x | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |
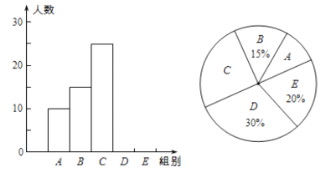
(1)统计表中的m=__,n=___;
(2)请补全频数分布直方图:
(3)在扇形统计图中,C组所对应扇形的圆心角的度数是______ ;
(4)已知该校共有1260名学生,如果听写汉字正确的个数少于24定为不合格,那么该校本次比赛不合格的学生人数大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)(﹣1.1)+(﹣3.9);(2)(﹣9)﹣(﹣7);(3)4![]() ﹣(+3.85)﹣(﹣3
﹣(+3.85)﹣(﹣3![]() )+(﹣3.15);(4)
)+(﹣3.15);(4)![]() ﹣|﹣1
﹣|﹣1![]() |﹣(+2
|﹣(+2![]() )﹣(﹣2.75)
)﹣(﹣2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了美化亮化某景点,在两条笔直的景观道![]() 、
、![]() 上,分别放置了
上,分别放置了![]() 、
、![]() 两盏激光灯,如图1所示,
两盏激光灯,如图1所示,![]() 灯发出的光束自
灯发出的光束自![]() 逆时针旋转至
逆时针旋转至![]() 便立即回转:
便立即回转:![]() 灯发出的光東自
灯发出的光東自![]() 逆时针旋转至
逆时针旋转至![]() 便立即回转,两灯不同断照射,
便立即回转,两灯不同断照射,![]() 们每秒转动
们每秒转动![]() 度,
度,![]() 每秒转动
每秒转动![]() 度,且满足
度,且满足![]() .若这两条景观道的道路是平行的,即
.若这两条景观道的道路是平行的,即![]() .
.

(1)求![]() 、
、![]() 的值:
的值:
(2)![]() 灯先转动
灯先转动![]() 秒,
秒,![]() 灯才开始转动,当
灯才开始转动,当![]() 灯转动
灯转动![]() 秒时,两灯的光東
秒时,两灯的光東![]() 和
和![]() 到达如图1所示的位置,试问
到达如图1所示的位置,试问和
![]() 是否平行?请说明理由:
是否平行?请说明理由:
(3)在(2)的情况下,当![]() 灯光束第一次达到
灯光束第一次达到![]() 之前,两灯的光束是否还能互相平行,如果还能互相平行,那么此时
之前,两灯的光束是否还能互相平行,如果还能互相平行,那么此时![]() 灯旋转的时间为______秒. (不要求写出解答过程)
灯旋转的时间为______秒. (不要求写出解答过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com