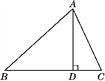
【题目】如图，在△ABC中，AD是BC边上的高，tanB＝cos∠DAC.
（1）求证：AC＝BD；
（2）若sin C＝
，BC＝12，求△ABC的面积．
【答案】（1）证明见解析；（2）△ABC的面积为48.
【解析】(1)∵AD是BC上的高，∴AD⊥BC．
∴∠ADB=90°，∠ADC=90°． …………………………………………1分
在Rt△ABD和Rt△ADC中，
∵
=
， 
=
…………………………………………3分
又已知
∴
=
．∴AC=BD． ………………………………4分
(2)在Rt△ADC中， 
，故可设AD=12k，AC=13k．
∴CD=
=5k．………………………………5分
∵BC=BD+CD，又AC=BD，
∴BC=13k+5k=18k ………………………………6分
由已知BC=12， ∴18k=12．∴k=
． ………………………………7分
∴AD=12k=12
=8． ……………………………8分
（1）在直角三角形中，表示
，根据它们相等，即可得出结论
（2）利用
和勾股定理表示出线段长，根据
，求出
长
科目：初中数学 来源： 题型：
【题目】如图，把Rt△ABC放在直角坐标系内，其中∠CAB＝90°，BC＝5，点A，B的坐标分别为(1，0)，(4，0)，将△ABC沿x轴向右平移，当点C落在直线y＝2x－6上时，线段BC扫过的面积为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠BAC=90°，AD⊥BC，垂足为D，则下面的结论中正确的个数为（ ）
①AB与AC互相垂直；
②AD与AC互相垂直；
③点C到AB的垂线段是线段AB；
④线段AB的长度是点B到AC的距离；
⑤线段AB是B点到AC的距离．
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=AC，点D为BC上一点，且AD=DC，过A，B，D三点作⊙O，AE是⊙O的直径，连结DE．
（1）求证：AC是⊙O的切线；
（2）若sinC=
，AC=6，求⊙O的直径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一项工程，甲队单独做需40天完成，若乙队先做30天后，甲、乙两队一起合做20天恰好完成任务，请问：
（1）乙队单独做需要多少天才能完成任务？
（2）现将该工程分成两部分，甲队做其中一部分工程用了x天，乙队做另一部分工程用了y天，若x; y都是正整数，且甲队做的时间不到15天，乙队做的时间不到70天，那么两队实际各做了多少天？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知 A（-4，0），B（0，2），C（0，-3），D（2，0）
（1）在图 1 中，画出四边形 ABDC，直接写出四边形 ABDC 的面积是 .
（2）点 E 是直线 AB 和 CD 的交点，求△ACE 的面积.
（3）点 P 的坐标为（0，p），△PAB 的面积大于△PCD 的面积，求 p 的取值范围.
图 1 备用图
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A，C，D，E在Rt△MON的边上，∠MON=90°，AE⊥AB且AE=AB，BC⊥CD且BC=CD，BH⊥ON于点H，DF⊥ON于点F，OM=12，OE=6，BH=3，DF=4，FN=8，图中阴影部分的面积为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：
售价x（元/千克） | … | 50 | 60 | 70 | 80 | … |
销售量y（千克） | … | 100 | 90 | 80 | 70 | … |
（1）求y与x的函数关系式；
（2）该批发商若想获得4000元的利润，应将售价定为多少元？
（3）该产品每千克售价为多少元时，批发商获得的利润w（元）最大？此时的最大利润为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
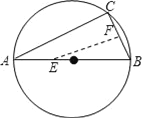
【题目】如图，AB是⊙O的直径，弦BC=2cm，F是弦BC的中点，∠ABC=60°．若动点E以2cm/s的速度从A点出发沿着ABA方向运动，设运动时间为t（s）（0≤t＜3），连接EF，当t为_____s时，△BEF是直角三角形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com