
【题目】已知 A(-4,0),B(0,2),C(0,-3),D(2,0)
(1)在图 1 中,画出四边形 ABDC,直接写出四边形 ABDC 的面积是 .
(2)点 E 是直线 AB 和 CD 的交点,求△ACE 的面积.
(3)点 P 的坐标为(0,p),△PAB 的面积大于△PCD 的面积,求 p 的取值范围.

图 1 备用图
【答案】(1)四边形见解析,面积为15;(2)22.25;(3) P<-3或-3<P<![]() 或P>7.
或P>7.
【解析】
描除A、B、C、D四点,然后顺次连接得到四边形,将四边形看成由△ACD和△ABD组成的,然后求两个三角形的面积,再求和即可.
通过A、B、C、D的坐标确定线段AB、CD所在的直线,然后求得交点E的坐标,最后进行求解即可.
设p的坐标为P(0,p),然后根据图形确定三角形的高和底,最后根据解一个含绝对值的方程即可.
解:(1) 描除A、B、C、D四点,然后顺次连接得到四边形ABCD,如图:
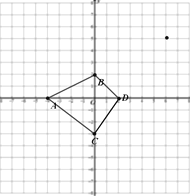
四边形ABDC的面积=△ABD+△ACD
=![]() ×6×2+
×6×2+![]() ×6×3
×6×3
=15
(2)设AB所在的直线为:y=kx+b
则有:![]() 解得:
解得:![]()
则AB所在的直线为:y=![]() x+2①
x+2①
同理CD所在的直线为:y=![]() ②
②
联立①②得:x=5,y=4.5
所以E的坐标为(5,4.5)
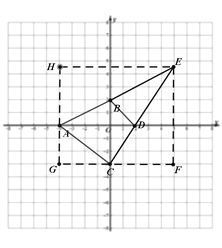
三角形AEC的面积为=四边形EFGH-△ECF-△AGC-△AHE
=9×7.5-![]() ×5×7.5-
×5×7.5-![]() ×4×3-
×4×3-![]() ×9×4.5
×9×4.5
=22.5
(3)设P(0,p),则如图:PB=|p-2|,PC=|p+3|,△PAB和△PCD的高分别为4和2
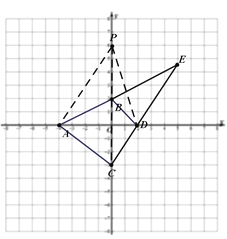
所以根据题意得:![]() ×|p-2|×4>
×|p-2|×4>![]() ×|p+3|×2,即2|P-2|>|p+3|
×|p+3|×2,即2|P-2|>|p+3|
解得:P<-3或-3<P<![]() 或P>7.
或P>7.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一种商品有大小两种包装,4 大盒、3 小盒共装 116 瓶;3 大盒、2 小盒共装 84 瓶,求大盒与小盒每盒各装多少瓶?
(2)一种商品有大中小三种包装,4 大盒、2 中盒、3 小盒共装 137 瓶;3 大盒、5 中盒、4 小盒共装171 瓶,一个顾客买了这种商品大中小各两盒,请问这个顾客买了这种商品多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
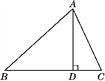
【题目】如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sin C=![]() ,BC=12,求△ABC的面积.
,BC=12,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织初二年级400名学生到威海参加拓展训练活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金250元,大客车每辆租金350元,请选出最省线的租车方案,并求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0).下列结论:①ab<0;②b2>4a;③0<a+b+c<2;④0<b<1;⑤当x>-1时,y>0.其中正确结论的个数是( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家工厂生产的办公桌和办公椅的质量、价格一致, 每张办公桌800元,每把椅子80元,甲、乙两个厂家推出各自销售的优惠方案:甲厂家,买张桌子送三把椅子:乙厂家,桌子和椅子全部按原价的8折优惠现某公司要购买3张办公桌和若干把椅子,若购买的椅子数为x把(![]() ) .
) .
(1)分别用含x的式子表示购买甲、乙两个厂家桌椅所需的金额:购买甲厂家的桌椅所需金额为_ ;购买乙厂家的桌椅所需金额为_
(2)该公司到哪家工厂购买更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(![]() ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.
其中说法正确的是( )
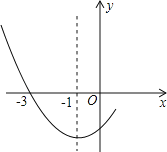
A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com