
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题
平面内的两条直线相交和平行两种位置关系,如图①,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因为∠BOD是△POD的外角,所以∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.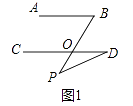
(1)将点P移到AB、CD内部,其余条件不变,如图②,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论; 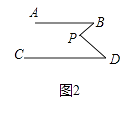
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,能否借助(1)中的图形与结论,找出图③中∠BPD、∠B、∠D、∠BQD之间有何数量关系?并说明理由. 
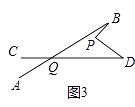
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得的线段CD的长.
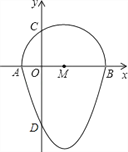
查看答案和解析>>
科目:初中数学 来源: 题型:
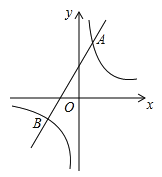
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点, 且y1>y2,求实数p的取值范围.
图象上的两点, 且y1>y2,求实数p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB:y=-x+b分别与x,y轴交于A(8,0)、B两点,过点B的直线交x轴轴负半轴于C,且OB:OC=4:3.
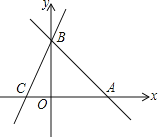
(1)求点B的坐标为 __________;
(2)求直线BC的解析式;
(3)动点M从C出发沿射线CA方向运动,运动的速度为每秒1个单位长度.设M运动t秒时,当t为何值时△BCM为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
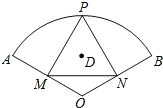
【题目】如图,扇形OAB的圆心角的度数为120°,半径长为4,P为弧AB上的动点,PM⊥OA,PN⊥OB,垂足分别为M、N,D是△PMN的外心.当点P运动的过程中,点M、N分别在半径上作相应运动,从点N离开点O时起,到点M到达点O时止,点D运动的路径长 ( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
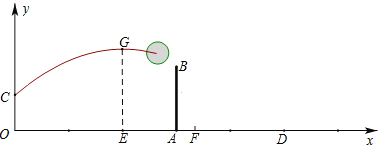
【题目】2016年里约奥运会,中国女排的姑娘们在郎平教练指导下,通过刻苦训练,取得了世界冠军,为国争光,如图,已知排球场的长度OD为18米,位于球场中线处球网的高度AB为2.43米,一队员站在点O处发球,排球从点O的正上方1.8米的C点向正前方飞出,当排球运行至离点O的水平距离OE为7米时,到达最高点G建立如图所示的平面直角坐标系.
(1)当球上升的最大高度为3.2米时,求排球飞行的高度y(单位:米)与水平距离x(单位:米)的函数关系式.(不要求写自变量x的取值范围).
(2)在(1)的条件下,对方距球网0.5米的点F处有一队员,他起跳后的最大高度为3.1米,问这次她是否可以拦网成功?请通过计算说明.
(3)若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com