
【题目】阅读材料,解决问题
平面内的两条直线相交和平行两种位置关系,如图①,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因为∠BOD是△POD的外角,所以∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.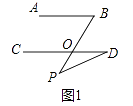
(1)将点P移到AB、CD内部,其余条件不变,如图②,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论; 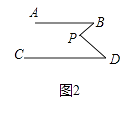
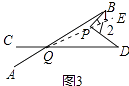
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,能否借助(1)中的图形与结论,找出图③中∠BPD、∠B、∠D、∠BQD之间有何数量关系?并说明理由. 
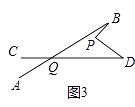
【答案】
(1)解:结论不成立,∠BPD=∠B+∠D.
作PQ∥AB,如图2,
∵AB∥CD,
∴AB∥PQ∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BPD=∠B+∠D
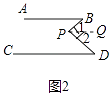
(2)解:∠BPD=∠B+∠D+∠BQD.理由如下:
连结QP并延长到E,如图3,
∵∠1=∠B+∠BQP,∠2=∠D+∠DQP,
∴∠1+∠2=∠B+∠BQP+∠D+∠DQP,
∴∠BPD=∠B+∠D+∠BQD.
【解析】(1)作PQ∥AB,根据平行线性质得AB∥PQ∥CD,则∠1=∠B,∠2=∠D,得出∠BPD=∠B+∠D;(2)连结QP并延长到E,根据三角形外角性质得∠1=∠B+∠BQP,∠2=∠D+∠DQP,然后把两式相加即可得到∠BPD=∠B+∠D+∠BQD.
【考点精析】通过灵活运用平行线的性质和旋转的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.


科目:初中数学 来源: 题型:
【题目】甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理过程中,环保部门每月初对两个城市的空气质量进行监测,连续10个月的空气污染指数如下图所示.其中,空气污染指≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.

(1)请填写下表:
平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
甲 | 80 | 1 | ||
乙 | 1060 | 80 |
(2)请回答下面问题:
①从平均数和中位数来分析,甲、乙两个城市的空气质量;
②从平均数和方差来分析,甲、乙两个城市的空气质量变化情况;
③根据折线图上两城市的空气污染指数的走势及优的情况来分析两城市治理环境污染的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市一月份的营业额为36万元,三月份的营业额为48万元,设每月的平均增长率为x,则可列方程为( )
A.48(1﹣x)2=36
B.48(1+x)2=36
C.36(1﹣x)2=48
D.36(1+x)2=48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与直线CD相交于点O,EO⊥AB,OF平分∠AOC, 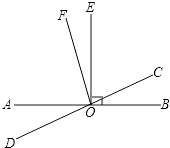
(1)请写出∠EOC的余角;
(2)若∠BOC=40°,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com