
【题目】甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理过程中,环保部门每月初对两个城市的空气质量进行监测,连续10个月的空气污染指数如下图所示.其中,空气污染指≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.

(1)请填写下表:
平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
甲 | 80 | 1 | ||
乙 | 1060 | 80 |
(2)请回答下面问题:
①从平均数和中位数来分析,甲、乙两个城市的空气质量;
②从平均数和方差来分析,甲、乙两个城市的空气质量变化情况;
③根据折线图上两城市的空气污染指数的走势及优的情况来分析两城市治理环境污染的效果.
【答案】(1)填表见解析;(2)乙;甲;乙
【解析】试题分析:(1)根据折线图,可得甲乙的数据,根据平均数、方差、中位数的计算方法,计算可得表中的数据;
(2)根据(1)的数据,依次比较可得答案,
①平均数相同,比较中位数可得,甲的中位数大于乙的中位数,进而可得答案,
②平均数相同,比较方差可得,甲的方差小于乙的方差,进而可得答案,
③根据折线图,分析两地的空气污染指数的走势,易得答案.
试题解析:(1)根据折线图,甲的数据依次为:110、90、100、80、90、60、90、50、70、60,有1次空气质量为优;乙的数据依次为:120、120、110、110、90、70、60、50、40、30;有3次空气质量为优;进而可得乙的平均数为:![]() (120+120+110+110+90+70+60+50+40+30)=80,甲的中位数为
(120+120+110+110+90+70+60+50+40+30)=80,甲的中位数为![]() (80+90)=85,填表可得:
(80+90)=85,填表可得:
平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
甲 | 80 | 340 | 85 | 1 |
乙 | 80 | 1060 | 80 | 3 |


科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,

(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
(3)玛丽在荡绳索过程中离地面的最低点的高度MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题
平面内的两条直线相交和平行两种位置关系,如图①,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因为∠BOD是△POD的外角,所以∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.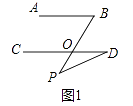
(1)将点P移到AB、CD内部,其余条件不变,如图②,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论; 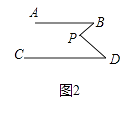
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,能否借助(1)中的图形与结论,找出图③中∠BPD、∠B、∠D、∠BQD之间有何数量关系?并说明理由. 
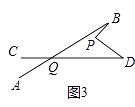
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)由大小相同的小立方块搭成的几何体如图1,请在图2的方格中画出该几何体的俯视图和左视图. 
(2)用小立方体搭一个几何体,使得它的俯视图和左视图与你在方格中所画的一致,则这样的几何体最少要个小立方块,最多要个小立方块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图a,在平面直角坐标系中,A、B坐标分别为(6,0),(0,6),P为线段AB上的一点.
(1) 如图a,若三角形OAP的面积是12,求点P的坐标;
(2)如图b,若P为AB的中点,点M,N分别是OA,OB边上的动点,点M从顶点A,点N从顶点O同时出发,且它们的速度都为1cm/s,则在M,N运动的过程中,线段PM,PN之间有何关系?并证明;
(3)如图c,若P为线段AB上异于A,B的任意一点,过B点作BD⊥OP,交OP,OA分别于F,D两点,E为OA上一点,且∠PEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com