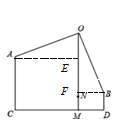
【题目】在一款名为超级玛丽的游戏中，玛丽到达一个高为10米的高台A，利用旗杆顶部的绳索，划过90°到达与高台A水平距离为17米，高为3米的矮台B，

（1）求高台A比矮台B高多少米？

（2）求旗杆的高度OM；

（3）玛丽在荡绳索过程中离地面的最低点的高度MN．

参考答案：

【答案】（1）7米；（2）OM=15m；（3）玛丽在荡绳索过程中离地面的最低点的高度MN为2米．

【解析】试题分析：（1）作差.(2) 作AE⊥OM，BF⊥OM,证明在△AOE和△OBF相似,可以计算出OE+OF长度，最后算出OM长度.(3)利用勾股定理求出半径长度，作差求MN长度.

试题解析：

（1）10-3=7(米）.

（2）作AE⊥OM于E,，BF⊥OM与F，

∵∠AOE+∠BOF=∠BOF+∠OBF=90°，

∴∠AOE=∠OBF，

在△AOE和△OBF中，

，

∴△AOE≌△OBF（AAS），

∴OE=BF，AE=OF，

即OE+OF=AE+BF=CD=17（m）

∵EF=EM﹣FM=AC﹣BD=10﹣3=7（m），

∴2EO+EF=17，

则2EO=10，

所以OE=5m，OF=12m，

所以OM=OF+FM=15m.

（3）由勾股定理得ON=OA=13，

所以MN=15﹣13=2（m）．

答：玛丽在荡绳索过程中离地面的最低点的高度MN为2米．

关闭