【题目】（本题满分10分）抛物线与x轴交与，两点，

（1）求该抛物线的解析式；

（2）设（1）中的抛物线与y轴交于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．

参考答案：

【答案】（1）y=-x2-2x+3；（2）存在Q（-1，2）.

【解析】试题分析：（1）把A（1,0）B（-3，0）代入然后解方程组即可；（2）因为线段AC的长固定不变，所以当AQ+CQ的长最小时△QAC的周长最小，根据轴对称的性质可知直线BC与对称轴的交点即为Q点，用待定系数法求直线BC解析式，把对称轴x=-1代入即可.

试题解析：解（1）把A（1,0）B（-3，0）代入到

3分

∴抛物线的解析式为y=-x2-2x+3 5分

（2）存在。 6分

过B、C作直线BC与对称轴x=-1的交点就是Q点，

设直线BC解析式为y=kx+b，把B（-3,0）C（0,3）代入到

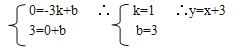
令XQ="-1" 得YQ=2 ∴Q（-1，2） 10分

关闭