
【题目】直线AB:y=-x+b分别与x,y轴交于A(8,0)、B两点,过点B的直线交x轴轴负半轴于C,且OB:OC=4:3.
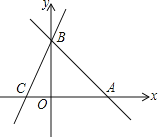
(1)求点B的坐标为 __________;
(2)求直线BC的解析式;
(3)动点M从C出发沿射线CA方向运动,运动的速度为每秒1个单位长度.设M运动t秒时,当t为何值时△BCM为等腰三角形.
【答案】(1)B(0,8);(2) y=![]() x+8;(3)10秒、
x+8;(3)10秒、![]() 秒或12秒.
秒或12秒.
【解析】试题分析:(1)把A的坐标代入y=-x+b,可得AB的解析式,令x=0,求出y的值,可得B的坐标;
(2)根据OB:OC=4:3,可得OC的长,根据待定系数法,可得函数解析式;
(3)根据等腰三角形的定义,分类讨论:MC=BC,MC=MB,BC=BM,①当MC=BC时,根据路程处以速度等于时间,可得答案;②当MC=MB时,根据两点间的距离,可得关于a的方程,根据解方程,可得a的值,再根据路程除以速度等于时间,可得答案;③当BC=BM时,根据线段垂直平分线的性质,可得MO的长,再根据两点间的距离,可得MC的长,根据路程除以速度等于时间,可得答案.
试题解析:解:(1)y=﹣x+b分别与x轴交于A(8、0),得:﹣8+b=0.解得b=8,即函数解析式为y=﹣x+8,当x=0时,y=8,B点坐标是(0,8);
(2)由OB:OC=4:3,BC=8,得:8:BC=4:3,解得BC=6,即C(﹣6,0),设直线BC的解析式为y=kx+b,图象经过点B,C,得: ![]() ,解得:
,解得: 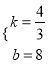 ,∴直线BC的解析式为y=
,∴直线BC的解析式为y=![]() x+8;
x+8;
(3)设M点坐标(a,0),由勾股定理得:BC=![]() =10,分三种情况讨论:
=10,分三种情况讨论:
①当MC=BC=10时,由路程处以速度等于时间,得10÷1=10(秒),即M运动10秒,△BCM为等腰三角形;
②当MC=MB时,MC2=MB2,即(a+6)2=a2+82,化简,得12a=28,解得a=![]() 即M(
即M(![]() ,0).MC=
,0).MC=![]() ﹣(﹣6)=
﹣(﹣6)=![]() +6=
+6=![]() ,由路程除以速度等于时间,得
,由路程除以速度等于时间,得![]() ÷1=
÷1=![]() (秒),即M运动
(秒),即M运动![]() 秒时,△BCM为等腰三角形;
秒时,△BCM为等腰三角形;
③当BC=BM时,得OC=OM=6,即MC=6﹣(﹣6)=6+6=12,由路程除以速度等于时间,得12÷1=12(秒),即M运动12秒时,△BCM为等腰三角形.
综上所述:t=10(秒),t=![]() (秒),t=12(秒)时,△BCM为等腰三角形.
(秒),t=12(秒)时,△BCM为等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,直线AB与直线CD相交于点O,EO⊥AB,OF平分∠AOC, 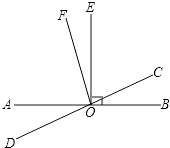
(1)请写出∠EOC的余角;
(2)若∠BOC=40°,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,图①、图②、图③均为顶点都在格点上的三角形(每个小方格的顶点叫格点),
(1)在图1中,图①经过一次 变换(填“平移”或“旋转”或“轴对称”)可以得到图②;
(2)在图1中,图③是可以由图②经过一次旋转变换得到的,其旋转中心是点 (填“A”或 “B”或“C”);
(3)在图2中画出图①绕点A顺时针旋转90°后的图④.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线MN交AB于点E,交AC于点D,且AC=15cm,△BCD的周长等于25cm. 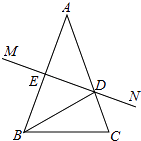
(1)求BC的长;
(2)若∠A=36°,并且AB=AC,求证:BC=BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com