
【题目】已知x=1是一元二次方程(a﹣2)x2+(a2﹣3)x﹣a+1=0的一个根,求a的值.
 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(1)求出m的值和抛物线与x轴的交点。
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y>0?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得的线段CD的长.
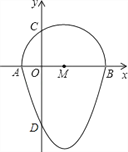
查看答案和解析>>
科目:初中数学 来源: 题型:
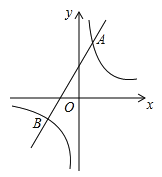
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点, 且y1>y2,求实数p的取值范围.
图象上的两点, 且y1>y2,求实数p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB:y=-x+b分别与x,y轴交于A(8,0)、B两点,过点B的直线交x轴轴负半轴于C,且OB:OC=4:3.
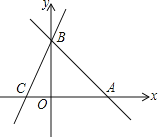
(1)求点B的坐标为 __________;
(2)求直线BC的解析式;
(3)动点M从C出发沿射线CA方向运动,运动的速度为每秒1个单位长度.设M运动t秒时,当t为何值时△BCM为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校的北大门是由相同菱形框架组成的伸缩电动推拉门,如图是大门关闭时的示意图,此时 菱形的边长为0.5m,锐角都是50°.求大门的宽(结果精确到0.01,参考数据:sin25°≈0.422 6,cos25°≈0.906 3).
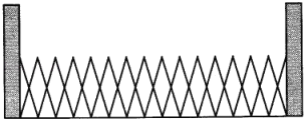
查看答案和解析>>
科目:初中数学 来源: 题型:
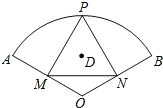
【题目】如图,扇形OAB的圆心角的度数为120°,半径长为4,P为弧AB上的动点,PM⊥OA,PN⊥OB,垂足分别为M、N,D是△PMN的外心.当点P运动的过程中,点M、N分别在半径上作相应运动,从点N离开点O时起,到点M到达点O时止,点D运动的路径长 ( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
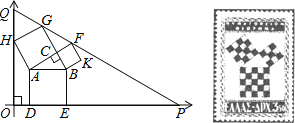
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2kx+k2﹣k=0(k>0).问x=0可能是方程一个根吗?若是,求出k值及方程的另一个根,若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com