
【题目】某市为了美化亮化某景点,在两条笔直的景观道![]() 、
、![]() 上,分别放置了
上,分别放置了![]() 、
、![]() 两盏激光灯,如图1所示,
两盏激光灯,如图1所示,![]() 灯发出的光束自
灯发出的光束自![]() 逆时针旋转至
逆时针旋转至![]() 便立即回转:
便立即回转:![]() 灯发出的光東自
灯发出的光東自![]() 逆时针旋转至
逆时针旋转至![]() 便立即回转,两灯不同断照射,
便立即回转,两灯不同断照射,![]() 们每秒转动
们每秒转动![]() 度,
度,![]() 每秒转动
每秒转动![]() 度,且满足
度,且满足![]() .若这两条景观道的道路是平行的,即
.若这两条景观道的道路是平行的,即![]() .
.

(1)求![]() 、
、![]() 的值:
的值:
(2)![]() 灯先转动
灯先转动![]() 秒,
秒,![]() 灯才开始转动,当
灯才开始转动,当![]() 灯转动
灯转动![]() 秒时,两灯的光東
秒时,两灯的光東![]() 和
和![]() 到达如图1所示的位置,试问
到达如图1所示的位置,试问和
![]() 是否平行?请说明理由:
是否平行?请说明理由:
(3)在(2)的情况下,当![]() 灯光束第一次达到
灯光束第一次达到![]() 之前,两灯的光束是否还能互相平行,如果还能互相平行,那么此时
之前,两灯的光束是否还能互相平行,如果还能互相平行,那么此时![]() 灯旋转的时间为______秒. (不要求写出解答过程)
灯旋转的时间为______秒. (不要求写出解答过程)
【答案】(1)![]() ;
;
(2)AM′和BP′平行,理由见解析;
(3)69秒或125秒或141秒.
【解析】
(1)利用非负数的性质构建方程组即可解决问题.
(2)AM′和BP′平行.证明∠AEB=∠MAM′即可.
(3)能,设A灯旋转时间为t秒,B灯光束第一次到达BQ需要180÷1=180(秒),推出t≤180-15,即t≤165.利用平行线的判定,构建方程解决问题即可.
解:(1)∵|a-4b|+(a+b-5)2=0,|a-4b|≥0,(a+b-5)2≥0,
![]()
解得![]()
(2)AM′和BP′平行,理由如下
由题意,得∠MAM′=5×4°=20°,∠PBP′=(15+5)×1°=20°,
∵MN∥QP,
∴∠AEB=∠PBP′=20°,
∴∠AEB=∠MAM′,
∴AM′∥BP′.
(3)t的值为69秒或125秒或141秒.
能,设A灯旋转时间为t秒,B灯光束第一次到达BQ需要180÷1=180(秒),
∴t≤180-15,即t≤165.
由题意,满足以下条件时,两灯的光束能互相平行:
①4t=15+t,解得t=5(不符合题意,舍去);
②4t-180+t+15=180,解得t=69;
③4t-360=15+t,解得t=125;
④4t-540+t+15=180,解得t=141;
⑤4t-720=15+t,解得t=245(不符合题意,舍去).
综上所述,满足条件的t的值为69秒或125秒或141秒.
故答案为:69秒或125秒或141秒.


科目:初中数学 来源: 题型:
【题目】如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着ABA方向运动,设运动时间为t(s)(0≤t<3),连接EF,当t为_____s时,△BEF是直角三角形.
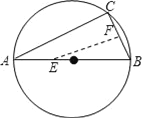
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节快到了,小明准备买粽子过节,若在超市购买![]() 盒甲品牌粽子和
盒甲品牌粽子和![]() 盒乙品牌粽子需支付
盒乙品牌粽子需支付![]() 元,而在某团购群购买
元,而在某团购群购买![]() 盒甲品牌粽子和
盒甲品牌粽子和![]() 盒乙品牌粽子需支付
盒乙品牌粽子需支付![]() 元对比发现,甲品牌粽子每盒的团购价相当于超市价的八折,乙品牌粽子每盒的团购价相当于超市价的七五折
元对比发现,甲品牌粽子每盒的团购价相当于超市价的八折,乙品牌粽子每盒的团购价相当于超市价的七五折
(1)甲、乙两种品牌粽子每盒的超市价分别是多少元?
(2)若购买甲品牌粽子![]() 盒,乙品牌粽子
盒,乙品牌粽子![]() 盒,则在团购群购买比在超市购买能省多少钱?
盒,则在团购群购买比在超市购买能省多少钱?
(3)小明要打算在团购群购买这两种品牌的粽子,其中乙品牌粽子比甲品牌粽子多![]() 盒,总花费不超过
盒,总花费不超过![]() 元,问小明最多能买多少盒甲品牌粽子?
元,问小明最多能买多少盒甲品牌粽子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区有两段长度相等的道路需硬化,现分别由甲、乙两个工程队同时开始施工.如图的线段和折线是两队前6天硬化的道路长y甲、y乙(米)与施工时间x(天)之间的函数图象

根据图象解答下列问题:
(1)直接写出y甲、y乙(米)与x(天)之间的函数关系式.
①当0<x≤6时,y甲= ;
②当0<x≤2时,y乙= ;当2<x≤6时,y乙= ;
(2)求图中点M的坐标,并说明M的横、纵坐标表示的实际意义;
(3)施工过程中,甲队的施工速度始终不变,而乙队在施工6天后,每天的施工速度提高到120米/天,预计两队将同时完成任务.两队还需要多少天完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张新是某县城中学的在校住宿生,开学初父母通过估算为他预存了一个学期的伙食费1600元,学校的学生食堂规定一天的伙食标准:早餐每人4元,中餐、晚餐只能各选一份价格如下表中的饭菜.
(1)请问该校每位住宿生一天的伙食费有几种可能的价格?其金额各是多少元?
(2)若张新选择(1)中一天的伙食费的两种价格,并计划用膳110天,且刚好用完预存款,那么他应有哪几种选择价格的方案?每种方案中两种价格各用膳多少天?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的点F处,并且FD∥BC,则CD的长是( )
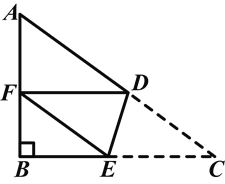
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com