
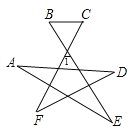
【题目】如图所示,∠1=65°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为___________.
科目:初中数学 来源: 题型:
【题目】(![]() 分)在菱形
分)在菱形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点.
上的一个动点.
(![]() )如图①,求
)如图①,求![]() 的最小值.
的最小值.
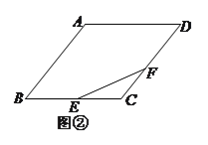
(![]() )如图②,若
)如图②,若![]() 也是
也是![]() 边上的一个动点,且
边上的一个动点,且![]() ,求
,求![]() 的最小值.
的最小值.
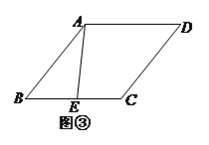
(![]() )如图③,若
)如图③,若![]() ,则在菱形内部存在一点
,则在菱形内部存在一点![]() ,使得点
,使得点![]() 分别到点
分别到点![]() 、点
、点![]() 、边
、边![]() 的距离之和最小.请你画出这样的点
的距离之和最小.请你画出这样的点![]() ,并求出这个最小值.
,并求出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
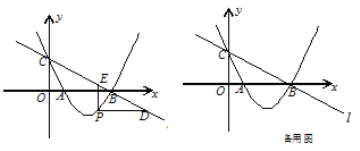
【题目】如图,直线![]() :
: ![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线![]() 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥![]() 轴交
轴交![]() 于点D,PE∥
于点D,PE∥![]() 轴交
轴交![]() 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线![]() 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
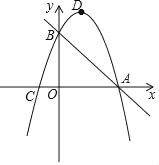
【题目】已知,如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)若点M为抛物线上一动点,是否存在点M,使△ACM与△ABC的面积相等?若存在,求点M的坐标;若不存在,请说明理由.
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,确定点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
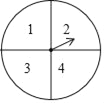
【题目】元旦期间,某商场设置了如图所示的幸运转盘,转盘分成4个大小相同的扇形,分别标有数学1,2,3,4,指针的位置固定,转盘可以自由转动,当转动的转盘停止后,其中的某个扇形会停在指针所指的位置(指针指向两个扇形的交线时,当作右边的扇形).商场规定:凡是参加抽奖的顾客均可转动转盘两次,如果两次转动中指针指缶扇形上的数字之和为8是一等奖,数字之和为7是二等奖,数字之和为6是三等奖,标号之和为其他数字则获得一份纪念品,请分别求出顾客抽中一、二、三等奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
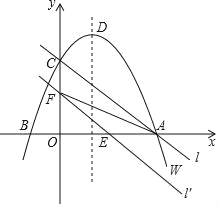
如图,在平面直角坐标系xOy中,抛物线W的函数表达式为y=﹣x2+2x+3,抛物线W与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,它的顶点为D,直线l经过A、C两点.
(1)求点A、B、C、D的坐标.
(2)将直线l向下平移m个单位,对应的直线为l′.
①若直线l′与x轴的正半轴交于点E,与y轴的正半轴交于点F,△AEF的面积为S,求S关于m的函数关系式,并写出自变量m的取值范围;
②求m的值为多少时,S的值最大?最大值为多少?
(3)若将抛物线W也向下平移m单位,再向右平移1个单位,使平移后得到的二次函数图象的顶点P落在△AOC的内部(不包括△AOC的边界),请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0).下列结论:①ab<0;②b2>4a;③0<a+b+c<2;④0<b<1;⑤当x>-1时,y>0.其中正确结论的个数是( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com