Question

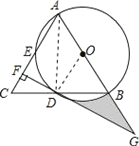
【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交线段BC，AC于点D，E，过点D作DF⊥AC，垂足为F，线段FD，AB的延长线相交于点G．

（1）求证：DF是⊙O的切线；

（2）若CF=2，DF=2，求图中阴影部分的面积．

Answer 1

【答案】（1）证明见解析（2）8﹣π

【解析】（1）连接AD、OD，由AB为直径可得出点D为BC的中点，由此得出OD为△BAC的中位线，再根据中位线的性质即可得出OD⊥DF，从而证出DF是⊙O的切线；

（2）CF=1，DF=，通过解直角三角形得出CD=2、∠C=60°，从而得出△ABC为等边三角形，再利用分割图形求面积法即可得出阴影部分的面积．

（1）证明：连接AD、OD，如图所示．

∵AB为直径，

∴∠ADB=90°，

∴AD⊥BC，∵AC=AB，

∴点D为线段BC的中点．

∵点O为AB的中点，

∴OD为△BAC的中位线，

∴OD∥AC，

∵DF⊥AC，

∴OD⊥DF，

∴DF是⊙O的切线．

（2）解：在Rt△CFD中，CF=2，DF=2，

∴tan∠C==，CD=4，

∴∠C=60°，

∵AC=AB，

∴△ABC为等边三角形，

∴AB=8．

∵OD∥AC，

∴∠DOG=∠BAC=60°，

∴DG=ODtan∠DOG=4，

∴S阴影=S△ODG﹣S扇形OBD=DGOD﹣πOB2=8﹣π