
【题目】如图,在等边△ABC中,AD⊥BC于D,若AB=4cm,AD=2 ![]() cm,E为AB的中点,P为AD上一点,PE+PB的最小值为 .
cm,E为AB的中点,P为AD上一点,PE+PB的最小值为 . 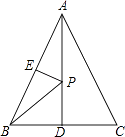
科目:初中数学 来源: 题型:
【题目】为了加强对校内外安全监控,创建荔湾平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
甲型 | 乙型 | |
价格(元/台) | a | b |
有效半径(米/台) | 150 | 100 |
(1)求a、b的值.
(2)若购买该批设备的资金不超过11000元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
(3)在(2)问的条件下,若要求监控半径覆盖范围不低于1600米,为了节约资金,请你设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的方格纸中,若多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形.记格点多边形内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为![]() ,其中m,n为常数.
,其中m,n为常数.
(1)在下面的方格中各画出一个面积为6的格点多边形,依次为三角形、平行四边形(非菱形)、菱形;
(2)利用(1)中的格点多边形确定m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题引入:
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);如图②,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示)
∠ACB,∠A=α,则∠BOC= (用α表示)
拓展研究:
(2)如图③,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.
∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
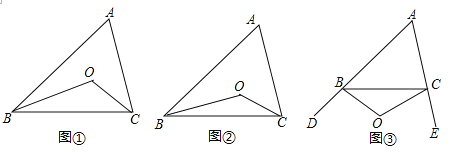
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子变形是因式分解的是( )
A.x2+5x+6=x(x+5)+6
B.x2﹣5x+6=(x﹣2)(x﹣3)
C.(x﹣2)(x﹣3)=x2﹣5x+6
D.x2﹣5x+6=(x+2)(x+3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com