
【题目】为了加强对校内外安全监控,创建荔湾平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
甲型 | 乙型 | |
价格(元/台) | a | b |
有效半径(米/台) | 150 | 100 |
(1)求a、b的值.
(2)若购买该批设备的资金不超过11000元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
(3)在(2)问的条件下,若要求监控半径覆盖范围不低于1600米,为了节约资金,请你设计一种最省钱的购买方案.
【答案】
(1)解:由题意得:
![]() ,
,
解得 ![]() ;
;
(2)解:设购买甲型设备x台,则购买乙型设备(15﹣x)台,依题意得
850x+700(15﹣x)≤11000,
解得x≤3 ![]() ,
,
∵两种型号的设备均要至少买一台,
∴x=1,2,3,
∴有3种购买方案:①甲型设备1台,乙型设备14台;②甲型设备2台,乙型设备13台;③甲型设备3台,乙型设备12台;
(3)解:依题意得:150x+100(15﹣x)≥1600,
解得x≥2,
∴x取值为2或3.
当x=2时,购买所需资金为:850×2+700×13=10800(元),
当x=3时,购买所需资金为:850×3+700×12=10950(元),
∴最省钱的购买方案为:购甲型设备2台,乙型设备13台.
【解析】(1)根据购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元,可列出方程组,然后解这个关于a、b的方程组即可求得a、b的值;
(2)可设购买甲型设备x台,则购买乙型设备(15-x)台,根据购买该批设备的资金不超过11000元列不等式,然后可求得x的取值范围,然后再结合x的取值范围进行方案设计即可;
(3)首先依据监控半径覆盖范围不低于1600米列出不等式,从而可求得x的取值范围,然后再根据x的值确定方案,最后,对所需资金进行比较,并作出选择即可.
【考点精析】利用一元一次不等式组的应用对题目进行判断即可得到答案,需要熟知1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要个小立方块.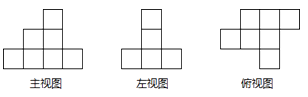
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出六个多项式:①x2+y2;②﹣x2+y2;③x2+2xy+y2;④x4﹣1;⑤x(x+1)﹣2(x+1);⑥m2﹣mn+ ![]() n2 . 其中,能够分解因式的是(填上序号).
n2 . 其中,能够分解因式的是(填上序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE. 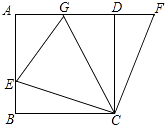
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,M为AB的中点,N为AD上的一点,且AN= ![]() AD,试猜测△CMN是什么三角形,请证明你的结论.(提示:正方形的四条边都相等,四个角都是直角)
AD,试猜测△CMN是什么三角形,请证明你的结论.(提示:正方形的四条边都相等,四个角都是直角) 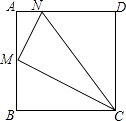
查看答案和解析>>
科目:初中数学 来源: 题型:
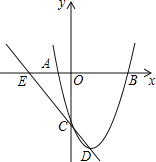
【题目】如图,已知抛物线经过点A(﹣2,0)、B(4,0)、C(0,﹣8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)直线CD交x轴于点E,过抛物线上在对称轴的右边的点P,作y轴的平行线交x轴于点F,交直线CD于M,使PM=![]() EF,请求出点P的坐标;
EF,请求出点P的坐标;
(3)将抛物线沿对称轴平移,要使抛物线与(2)中的线段EM总有交点,那么抛物线向上最多平移多少个单位长度,向下最多平移多少个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果用“a=b”表示一个等式,c表示一个整式,d表示一个数,那么等式的第一条性质就可以表示为“a±c=b±c”,以下借助符号正确的表示出等式的第二条性质的是( )
A. ac=bd,a÷c=b÷d
B. ad=b÷d,a÷d=bd
C. ad=bd,a÷d=b÷d
D. ad=bd,a÷d=b÷d(d≠0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com