
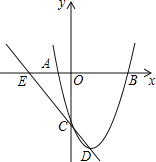
【题目】如图,已知抛物线经过点A(﹣2,0)、B(4,0)、C(0,﹣8).
(1)求抛物线的解析式及其顶点D的坐标;
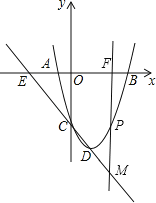
(2)直线CD交x轴于点E,过抛物线上在对称轴的右边的点P,作y轴的平行线交x轴于点F,交直线CD于M,使PM=![]() EF,请求出点P的坐标;
EF,请求出点P的坐标;
(3)将抛物线沿对称轴平移,要使抛物线与(2)中的线段EM总有交点,那么抛物线向上最多平移多少个单位长度,向下最多平移多少个单位长度.
【答案】(1)![]() ,顶点D的坐标为(1,﹣9);(2)P(2,﹣8);(3)抛物线向上最多平移
,顶点D的坐标为(1,﹣9);(2)P(2,﹣8);(3)抛物线向上最多平移![]() 个单位长度,向下最多平移72个单位长度.
个单位长度,向下最多平移72个单位长度.
【解析】
试题分析:(1)由于抛物线与x轴的两个交点已知,抛物线的解析式可设成交点式:y=a(x+2)(x﹣4),然后将点C的坐标代入就可求出抛物线的解析式,再将该解析式配成顶点式,即可得到顶点坐标.
(2)先求出直线CD的解析式,再求出点E的坐标,然后设点P的坐标为(m,n),从而可以用m的代数式表示出PM、EF,然后根据PM=![]() EF建立方程,就可求出m,进而求出点P的坐标.
EF建立方程,就可求出m,进而求出点P的坐标.
(3)先求出点M的坐标,然后设平移后的抛物线的解析式为![]() ,然后只需考虑三个临界位置(①向上平移到与直线EM相切的位置,②向下平移到经过点M的位置,③向下平移到经过点E的位置)所对应的c的值,就可以解决问题.
,然后只需考虑三个临界位置(①向上平移到与直线EM相切的位置,②向下平移到经过点M的位置,③向下平移到经过点E的位置)所对应的c的值,就可以解决问题.
试题解析:(1)根据题意可设抛物线的解析式为y=a(x+2)(x﹣4).
∵点C(0,﹣8)在抛物线y=a(x+2)(x﹣4)上,∴﹣8a=﹣8,∴a=1,∴y=(x+2)(x﹣4)=![]() ,即
,即![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ,顶点D的坐标为(1,﹣9);
,顶点D的坐标为(1,﹣9);
(2)如图,设直线CD的解析式为y=kx+b,∴![]() ,解得:
,解得:![]() ,∴直线CD的解析式为y=﹣x﹣8.当y=0时,﹣x﹣8=0,则有x=﹣8,∴点E的坐标为(﹣8,0).
,∴直线CD的解析式为y=﹣x﹣8.当y=0时,﹣x﹣8=0,则有x=﹣8,∴点E的坐标为(﹣8,0).
设点P的坐标为(m,n),则PM=![]() =
=![]() ,EF=m﹣(﹣8)=m+8.
,EF=m﹣(﹣8)=m+8.
∵PM=![]() EF,∴
EF,∴![]() .整理得:
.整理得:![]() ,∴(5m+4)(m﹣2)=0,解得:m=
,∴(5m+4)(m﹣2)=0,解得:m=![]() 或m=2.∵点P在对称轴x=1的右边,∴m=2.此时,n=
或m=2.∵点P在对称轴x=1的右边,∴m=2.此时,n=![]() ﹣2×2﹣8=﹣8,∴点P的坐标为(2,﹣8);
﹣2×2﹣8=﹣8,∴点P的坐标为(2,﹣8);
(3)当m=2时,y=﹣2﹣8=﹣10,∴点M的坐标为(2,﹣10).
设平移后的抛物线的解析式为![]() ,①若抛物线
,①若抛物线![]() 与直线y=﹣x﹣8相切,则方程
与直线y=﹣x﹣8相切,则方程![]() 即
即![]() 有两个相等的实数根,∴1﹣4×1×c=0,∴c=
有两个相等的实数根,∴1﹣4×1×c=0,∴c=![]() ;
;
②若抛物线![]() 经过点M,则有
经过点M,则有![]() ,∴c=﹣2;
,∴c=﹣2;
③若抛物线![]() 经过点E,则有
经过点E,则有![]() ,∴c=﹣72.
,∴c=﹣72.
综上所述:要使抛物线与(2)中的线段EM总有交点,抛物线向上最多平移![]() 个单位长度,向下最多平移72个单位长度.
个单位长度,向下最多平移72个单位长度.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
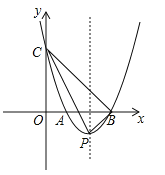
【题目】如图,在平面直角坐标系中,抛物线![]() 经过点(﹣1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).
经过点(﹣1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).
(1)求抛物线的解析式;
(2)若抛物线与y轴交于点C,顶点为点P,求△CPB的面积.
注:抛物线![]() (a≠0)的顶点坐标是(
(a≠0)的顶点坐标是(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强对校内外安全监控,创建荔湾平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
甲型 | 乙型 | |
价格(元/台) | a | b |
有效半径(米/台) | 150 | 100 |
(1)求a、b的值.
(2)若购买该批设备的资金不超过11000元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
(3)在(2)问的条件下,若要求监控半径覆盖范围不低于1600米,为了节约资金,请你设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
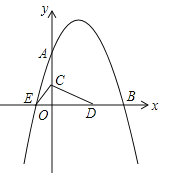
【题目】如图,已知抛物线![]() 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某陶瓷商,为了促销决定卖一只茶壶,赠一只茶杯。某人共付款162元,买得茶壶茶杯共36只,已知每只茶壶15元,每只茶杯3元,问其中茶壶、茶杯各多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题引入:
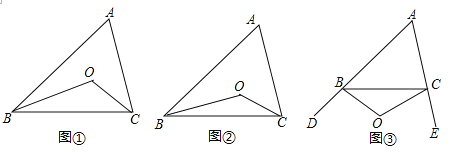
(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);如图②,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示)
∠ACB,∠A=α,则∠BOC= (用α表示)
拓展研究:
(2)如图③,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.
∠ECB,∠A=α,请猜想∠BOC= (用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com