
【题目】如图,等腰△ABC底边BC的长为4cm,面积是12cm2 , 腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最小值为cm. 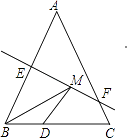
【答案】8
【解析】解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC= ![]() BCAD=
BCAD= ![]() ×4×AD=12,解得AD=6cm,
×4×AD=12,解得AD=6cm,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+ ![]() BC=6+
BC=6+ ![]() ×4=6+2=8cm.
×4=6+2=8cm.
所以答案是:8.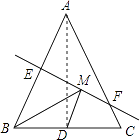
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】改革开放四十年以来,中国每天都在发生新的变化.目前,我省重大新兴产业基地、工程和专项在建及储备项目共1656个,总投资9364亿元.数据9364亿用科学记数法可表示为( )
A.9364×108B.9364×109C.9.364×1011D.9.364×1012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
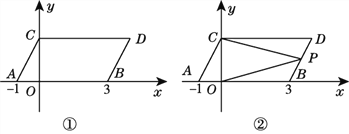
【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变,②
的值不变,②![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com