
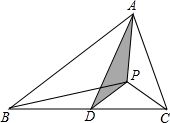
 如图,△ABC中,D是BC边的中点,已知点P是△ACD内一点,己知△ACP的面积为7,△ABP的面积为13,则阴影部分的面积为3.
如图,△ABC中,D是BC边的中点,已知点P是△ACD内一点,己知△ACP的面积为7,△ABP的面积为13,则阴影部分的面积为3. 分析 先由“D是BC边中点”,得出△ABD的面积=△ACD的面积=$\frac{1}{2}$△ABC的面积,△CBD的面积=△BPD的面积,设△BPD的面积=△CPD的面积=x,表示出△ABC的面积,进而解决问题.
解答 解:∵D是BC边中点,
∴△ABD的面积=△ACD的面积=$\frac{1}{2}$△ABC的面积,
△CBD的面积=△BPD的面积,
设△BPD的面积=△CPD的面积=x,
则△ABC的面积=2x+13+7=2x+20,
∴△ABD的面积=(2x+20)÷2=x+10,
∴阴影部分的面积=△BPD的面积+△BPD的面积-△ABD的面积
=13+x-(10+x)
=13-10
=3.
故答案为:3.
点评 本题考查了三角形的面积;此题解答的关键在于运用三角形面积与底的正比关系求出面积之间的关系,并逐步解决问题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
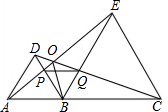 如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是①③④(填写序号).
如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是①③④(填写序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
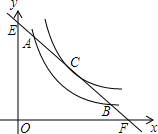 如图,直线y=-x+m与y=$\frac{4}{x}$只有唯一公共点C,与y=$\frac{k}{x}$交于A、B,且AC=$\frac{3}{2}$$\sqrt{2}$,求k.
如图,直线y=-x+m与y=$\frac{4}{x}$只有唯一公共点C,与y=$\frac{k}{x}$交于A、B,且AC=$\frac{3}{2}$$\sqrt{2}$,求k.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com