
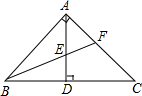
 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BF交AD于点E,交AC于点F,且AE=AF,求证:BF平分∠ABC.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BF交AD于点E,交AC于点F,且AE=AF,求证:BF平分∠ABC. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
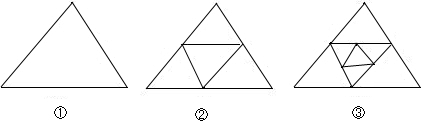
| 图形编号 | ① | ② | ③ | ④ | ⑤ | … |
| 三角形个数 | 1 | 5 | 9 | 13 | 17 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一次军演中,一艘潜艇在海面以下600米的点A处测得仰角为30°的正前方海面上C处有一艘可疑军舰,潜艇在同一深度以300$\sqrt{3}$米/分的速度直线航行20分钟到达点B处.测得该军舰在仰角为60°正前方的海面上D处.求军舰的平均速度.(精确到米,参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732,$\sqrt{5}$=2.236)
如图,在一次军演中,一艘潜艇在海面以下600米的点A处测得仰角为30°的正前方海面上C处有一艘可疑军舰,潜艇在同一深度以300$\sqrt{3}$米/分的速度直线航行20分钟到达点B处.测得该军舰在仰角为60°正前方的海面上D处.求军舰的平均速度.(精确到米,参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732,$\sqrt{5}$=2.236)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com