Question

7．△ABC是等腰三角形，∠ABC=120°，O为AC的中点，将等边△OEF的顶点放在点O处，OE、OF分别交AB、BC于点M、N．
（1）如图1，当BM=BN，求证：OM=ON．
（2）如图2，若△OEF的边长为6，M为OE的中点，点G在边EF上，点H在边OF上，将FGH沿着GH折叠，使点F落在△OEF内部一点F′处，F′H所在直线垂直EO于Q，F′Q=QO，QH=$\sqrt{3}$QO，求MQ的长．
（3）将图1中的△OEF绕O点顺时针旋转至图3所示的位置，写出线段BM，BN与AB之间的数量关系，并进行证明．

Answer 1

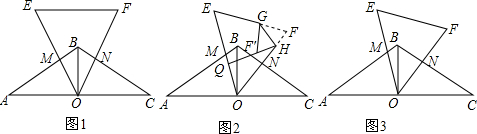
分析 （1）根据题意，可求得∠A=∠C，AO=CO，BM=BN，根据全等三角形的判定，即可证明△AOM≌△CON，则结论得证；
（2）根据Rt△OHQ中，∠EOF=60°，可用含OQ的式子表示出OH，即可表示出FH，根据$QH=\sqrt{3}OQ$，F′Q=OQ，用含OQ的式子表示出F′H，根据题意，可知FH=F′H，列出方程，即可求得OQ，则可求得MQ；
（3）取AB得中点G，连接OG，根据直角三角形的中线定理，及30°的直角三角形的性质，证得OQ=OB，根据∠GOB=∠MON=60°，证得∠GOM=∠NOB，根据全等三角形的判定，即可证明GM=BN，即可证得BM、BN、AB的关系．

解答 （1）证明：∵△ABC是等腰三角形，O是中点，
∴∠A=∠C，AO=CO，AB=BC，
又∵BM=BN，
∴AB-BM=BC-BN，
即AM=CN，
在△AOM和△CON中，
$\left\{\begin{array}{l}{0A=0C}\\{∠A=∠C}\\{AM=CN}\end{array}\right.$，
∴△AOM≌△CON，
∴OM=ON；
（2）解：∵△FGH沿着GH折叠得到△F′GH，
∴F′H=FH，
∵HQ⊥OM，
∴∠HQO=90°，
∵△OEF是等边三角形，
∴∠EOF=60°，
在Rt△OQH中，∠EOF=60°，
∴OH=$\frac{OQ}{cos60°}$=2OQ，
∵OH=$\sqrt{3}$OQ，F′Q=OQ，
∴F′H=$\sqrt{3}$OQ-OQ=（$\sqrt{3}$-1）OQ，
∵OF=6，FH=6-2OQ，
∴（$\sqrt{3}$-1）OQ=6-2OQ，
解得：OQ=3$\sqrt{3}$-3，
∵OE=6，M是OE的中点，
∴OM=3，
∴MQ=MO-OQ=3-（3$\sqrt{3}$-3）=6-3$\sqrt{3}$；
（3）BM+BN=$\frac{1}{2}$AB；
证明如下：如右图，取AB的中点G，连接OG，则OG=AG=BG，
∵△ABC是等腰三角形，∠ABC=120°，O是AC的中点，
∴∠A=30°，∠ABO=$\frac{1}{2}$∠ABC=60°，
在△AOB中，∠A=30°，
∴OB=AG=BG，
∴OG=OB，∠GOB=60°，即∠1+∠2=60°，
由等边△EOF，得：∠EOF=60°，即∠2+∠3=60°，
∴∠1=∠3，
在△OGM和△OBN中
$\left\{\begin{array}{l}{∠1=∠3}\\{OG=OB}\\{∠OGM=∠OBN}\end{array}\right.$，
∴△OGM≌△OBN（ASA），
∴GM=BN，
∴BM+BN=BM+GM=$\frac{1}{2}$AB．

点评 本题主要考查了全等三角形的性质和判定、等腰三角形的性质、勾股定理的综合应用，第（2）小题，用含有OQ的式子表示FH和F′H是解决本小题的关键；第（3）小题，解题的关键是将线段BM、BN，转化到线段AB上．