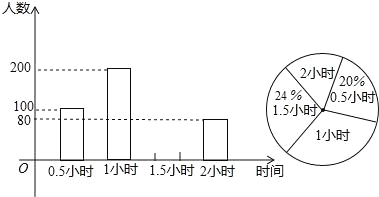
【题目】为了解学生参加户外活动的情况，对部分学生参加户外活动的时间进行抽查调查，并将调查结果绘制成如下两幅不完整的统计图，根据图示，请回答下列问题：

（1）被抽查的学生数是 ，并补全图中的频数分布直方图；

（2）扇形统计图中，户外活动时间为2小时部分对应的圆心角的度数为 ．

（3）户外活动时间的中位数是 ．

参考答案：

【答案】（1）500人，补图参见解析；（2）57.6°；（3）1．

【解析】

试题分析：（1）根据户外活动0.5小时的有100人，占总体的20%，由总数=某组频数÷频率计算即可解答；由1.5小时占总体的24%，求出户外活动1.5小时的有多少人，即可补全直方图；（2）根据扇形圆心角的度数=360×2小时人数占总体的比例即可解答；（3）共有500个数据，根据中位数的定义，找出第250与第251名的数据即可解答．

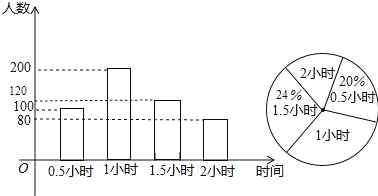
试题解析：（1）因为户外活动0.5小时的有100人，占总体的20%，所以调查人数=100÷20%=500（人）；1.5小时占总体的24%，所以户外活动1.5小时的有500×24%=120人，补全频数分布直方图如下：

；

（2）根据扇形圆心角的度数=360×2小时人数占总体的比例，求出户外活动时间2小时的扇形圆心角的度数=×360°=57.6°；（3）共有500个数据，根据中位数的定义，找出第250与第251名的数据都是1小时，所以户外活动时间的中位数为（1+1）÷2=1小时．故答案为：500，57.6，1．

关闭