
【题目】如图,在正方形ABCD中,G是BC上任意一点,连结AG,DE⊥AG于点E,BF∥DE交AG于点F,探究线段DE,BF,EF三者之间的数量关系,并说明理由.

【答案】DE=BF+EF
【解析】试题分析:DE=BF+EF,根据已知条件易证△ABF≌△DAE,由全等三角形的性质可得BF=AE,AF=DE,根据图中相关线段的和差关系得到DE=BF+EF.
试题解析:
DE=BF+EF.理由如下:
∵四边形ABCD是正方形,
∴AB=DA,∠DAB=∠ABC=90°.
∵DE⊥AG于点E,BF∥DE交AG于点F,
∴∠DEA=∠DEF=∠AFB=90°,
∴∠ADE+∠DAE=90°.
∵∠DAE+∠BAF=90°,
∴∠ADE=∠BAF.
在△ABF和△DAE中,
∵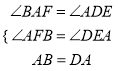
∴△ABF≌△DAE(AAS).
∴BF=AE,AF=DE.
∵AF=AE+EF,
∴DE=BF+EF.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
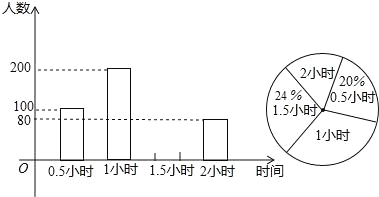
【题目】为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽查调查,并将调查结果绘制成如下两幅不完整的统计图,根据图示,请回答下列问题:
(1)被抽查的学生数是 ,并补全图中的频数分布直方图;
(2)扇形统计图中,户外活动时间为2小时部分对应的圆心角的度数为 .
(3)户外活动时间的中位数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次地震期间,为了紧急安置60名地震灾民,需要搭建可容纳6人或4人的帐篷,若所搭建的帐篷恰好(即不多不少)能容纳这60名灾民,则不同的搭建方案有 种.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,过点O分别作OE⊥AB,OF⊥AC,E,F分别是垂足.
判断![]() 与
与![]() 的关系______;
的关系______;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC一定成立吗?请画图表示,不需证明.
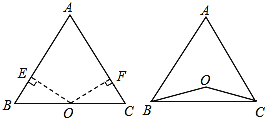
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线的方程C1: ![]() (m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(1)若抛物线C1过点M(2, 2),求实数m的值;
(2)在(1)的条件下,求△BCE的面积;
(3)在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标;
(4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2﹣2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为( )
A.y=(x﹣2)2+3
B.y=(x﹣2)2+5
C.y=x2﹣1
D.y=x2+4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com