
【题目】如图,在平面直角坐标系中,OA=OB=OC=6,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的![]() .
.
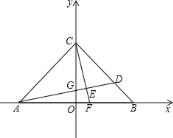
(1)求点D的坐标;
(2)过点C作CE⊥AD,交AB交于F,垂足为E.
①求证:OF=OG;
②求点F的坐标。
(3)在(2)的条件下,在第一象限内是否存在点P,使△CFP为等腰直角三角形?若存在,直接写出点P坐标;若不存在,请说明理由。
【答案】(1) (4,2)
(2)①见解析 ②(1.2,0)
(3)存在,P(6,7.2),(7.2,1.2),(3.6,3.6).
【解析】
(1)作DH⊥AB于H,由OA=OB=OC=6,就可以得出∠ABC=45°,由三角形的面积公式就可以求出DH的值,就可以求出BH的值,从而求出D的坐标;
(2)①根据OA=OC,再根据直角三角形的性质就可以得出△AOG≌△COF,就可以得出OF=OG;
②由△AOG∽△AHD就可以得出OG的值,就可以求出F的坐标.
(3)根据条件作出图形图1,作PH⊥OC于H,PM⊥OB于M,由△PHC≌△PMF就可以得出结论,图2,作PH⊥OB于H,由△COF≌△PHF就可以得出结论,图3,作PH⊥OC于H,由△COF≌△PHC就可以得出结论.
(1)作DH⊥AB于H,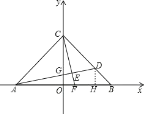
∴∠AHD=∠BHD=90°.
∵OA=OB=OC=6,
∴AB=12,
∴S△ABC=![]() =36
=36
∵△ABD的面积为△ABC面积的![]() .
.
∴![]() ,
,
∴DH=2.
∵OC=OB,
∴∠BCO=∠OBC.
∵∠BOC=90°,
∴∠BCO=∠OBC=45°,
∴∠HDB=45°,
∴∠HDB=∠DBH,
∴DH=BH.
∴BH=2.
∴OH=4,
∴D(4,2);
(2)①∵CE⊥AD,
∴∠CEG=∠AEF=90°,
∵∠AOC=∠COF=90°,
∴∠COF=∠AEF=90°
∴∠AFC+∠FAG=90°,∠AFC+∠OCF=90°,
∴∠FAG=∠OCF.
在△AOG和△COF中
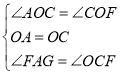
∴△AOG≌△COF(ASA),
∴OF=OG;
②∵∠AOG=∠AHD=90°,
∴OG∥DH,
∴△AOG∽△AHD,
∴![]() ,
,
∴![]()
∴OG=1.2.
∴OF=1.2.
∴F(1.2,0)
(3)如图1,当∠CPF=90°,PC=PF时,作PH⊥OC于H,PM⊥OB于M
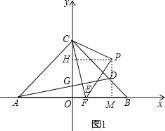
∴∠PHC=∠PHO=∠PMO=∠PMB=90°.
∵∠BOC=90°,
∴四边形OMPH是矩形,
∴∠HPM=90°
∴∠HPF+∠MPF=90°
∵∠CPF=90°,
∴∠CPH+∠HPF=90°
∵∠CPH=∠FPM.
在△PHC和△PMF中
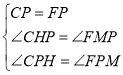
∴△PHC≌△PMF(AAS),
∴CH=FM.HP=PM,
∴矩形HPMO是正方形,
∴HO=MO=HP=PM.
∵CO=OB,
∴COOH=OBOM,
∴CH=MB,
∴FM=MB.
∵OF=1.2,
∴FB=4.8,
∴FM=2.4,
∴OM=3.6
∴PM=3.6,
∴P(3.6,3.6);
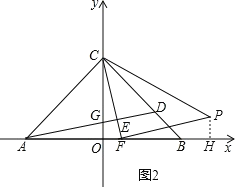
图2,当∠CFP=90°,PF=CF时,作PH⊥OB于H,
∴∠OFC+∠PFH=90°,∠PHF=90°
∴∠PFH+∠FPH=90°
∴∠OFC=∠HPF.
∵∠COF=90°,
∴∠COF=∠FHP.
在△COF和△PHF中
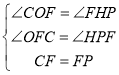
∴△COF≌△PHF(AAS),
∴OF=HP,CO=FH,
∴HP=1.2,FH=6,
∴OH=7.2,
∴P(7.2,1.2);
图3,当∠FCP=90°,PC=CF时,作PH⊥OC于H,
∴∠CHP=90°,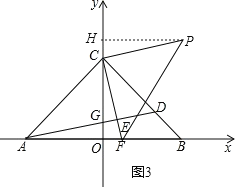
∴∠HCP+∠HPC=90°.
∵∠FCP=90°,
∴∠HCP+∠OCF=90°,
∴∠OCF=∠HCP.
∵∠FOC=90°,
∴∠FOC=∠CHP.
在△COF和△PHC中
 ,
,
∴△COF≌△PHC(AAS),
∴OF=HC,OC=HP,
∴HC=1.2,HP=6,
∴HO=7.2,
∴P(6,7.2),
∴P(6,7.2),(7.2,1.2),(3.6,3.6).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°.
(1)如图1,点E为线段AB的中点,连接DE,CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(M不与A,C重合),以AM为边,构造如图所示等边三角形AMN,线段MN与AD交于点G,连接NC,DM,Q为线段NC的中点,连接DQ,MQ,求证:DM=2DQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,∠ABC+∠ADC=180,连接AC,BD.
(1)如图1,当∠ACD=∠CAD=45时,求∠CBD的度数;
(2)如图2,当∠ACD=∠CAD=60时,求证:AB+BC=BD;
(3)如图3,在(2)的条件下,过点C作CK⊥BD于点K,在AB的延长线上取点F,使∠FCG=60,过点F作FH⊥BD于点H,BD=8,AB=5,GK=![]() ,求BH的长。
,求BH的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )

A. 4次 B. 3次 C. 2次 D. 1次
查看答案和解析>>
科目:初中数学 来源: 题型:
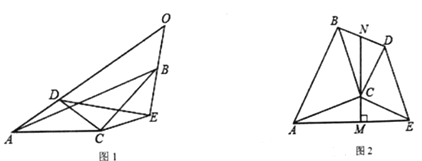
【题目】在△ABC和△DCE中,CA=CB,CD=CE,∠CAB= ∠CED=α.
(1)如图1,将AD、EB延长,延长线相交于点0.
①求证:BE= AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N.求证:N是BD的中点.
注:第(2)问的解答过程无需注明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道习题:如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.
(1)证明:RP=RQ;
(2)请探究下列变化:
A、变化一:交换题设与结论.已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.证明:RQ为⊙O的切线.

B、变化二:运动探求. ①如图2,若OA向上平移,变化一中结论还成立吗?(只交待判断) 答:_________.
②如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,原题中的结论还成立吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com