
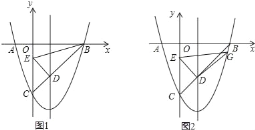
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœþy=x2©Å2x©Å3æ≠π˝x÷·…œµƒA£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨œþ∂ŒBC”Î≈◊ŒÔœþµƒ∂‘≥∆÷·œýΩª”⁄µ„D£¨µ„EŒ™y÷·…œµƒ“ª∏ˆ∂ص„£Æ
£®1£©«Û÷±œþBCµƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢«Û≥ˆµ„Dµƒ◊¯±Í£ª
£®2£©…˵„Eµƒ◊ð◊¯±ÍŒ™Œ™m£¨‘⁄µ„Eµƒ‘À∂Øπ˝≥Ã÷–£¨µ±°˜BDE÷–Œ™∂€Ω«»˝Ω«–Œ ±£¨«Ûmµƒ»°÷µ∑∂Œß£ª
£®3£©»ÁÕº2£¨¡¨Ω·DE£¨Ω´…‰œþDE»∆µ„DÀ≥ ±’Î∑ΩœÚ–˝◊™90°„£¨”Î≈◊ŒÔœþΩªµ„Œ™G£¨¡¨Ω·EG£¨DGµ√µΩRt°˜GED£Æ‘⁄µ„Eµƒ‘À∂Øπ˝≥Ã÷–£¨ «∑ҥʑ⁄’‚—˘µƒRt°˜GED£¨ πµ√¡Ω÷±Ω«±þ÷Ʊ»Œ™2£∫1£ø»Áπ˚¥Ê‘⁄£¨«Û≥ˆ¥À ±µ„Gµƒ◊¯±Í£ª»Áπ˚≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£© y=x©Å3£¨Dµ„◊¯±ÍŒ™£®1£¨©Å2£©£ª£®2£© m£æ3ªÚm£º©Å1«“m°Ÿ©Å3£ª£®3£©¥Ê‘⁄£Æ Gµ„◊¯±ÍŒ™£®1![]() £©ªÚ£®3£¨0£©ªÚ£®1
£©ªÚ£®3£¨0£©ªÚ£®1![]() £©ªÚ£®©Å1£¨0£©£Æ
£©ªÚ£®©Å1£¨0£©£Æ
°æΩ‚Œˆ°ø
£®1£©œ»∏˘æð≈◊ŒÔœþ”Îx÷·µƒΩªµ„Œ «Û≥ˆA£®©Å1£¨0£©£¨B£®3£¨0£©£¨¿˚”√∂‘≥∆–‘ø…µ√≈◊ŒÔœþµƒ∂‘≥∆÷·Œ™÷±œþx=1£¨‘Ÿ«Û≥ˆC£®0£¨©Å3£©£¨»ª∫Û¿˚”√¥˝∂®œµ ˝∑®«Û÷±œþBCµƒΩ‚Œˆ Ω£ªµ±x=1 ±£¨y=x©Å3=©Å2£¨‘ÚDµ„◊¯±ÍŒ™£®1£¨©Å2£©£ª
£®2£©»ÁÕº1£¨œ»≈–∂œ°˜OBCŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨‘Ú°œOCB=°œOBC=45°„£¨‘Ÿº∆À„≥ˆCD![]() £¨»ª∫ÛÕ®π˝«Û≥ˆ°˜BDEŒ™÷±Ω«»˝Ω«–Œ ±mµƒ÷µ¿¥»∑∂®°˜BDEŒ™∂€Ω«»˝Ω«–Œ ±mµƒ»°÷µ∑∂Œß£ª
£¨»ª∫ÛÕ®π˝«Û≥ˆ°˜BDEŒ™÷±Ω«»˝Ω«–Œ ±mµƒ÷µ¿¥»∑∂®°˜BDEŒ™∂€Ω«»˝Ω«–Œ ±mµƒ»°÷µ∑∂Œß£ª
£®3£©∑÷¿ýÃ÷¬€£∫¢Ÿµ±µ„G‘⁄∂‘≥∆÷·”“≤ýµƒ≈◊ŒÔœþ…œ ±£¨»ÁÕº2£¨◊˜DF°Õy÷·”⁄F£¨GH°ÕDF”⁄H£¨…ËG£®t£¨t2©Å2t©Å3£©£¨‘ÚGH=t2©Å2t©Å3©Å£®©Å2£©=t2©Å2t©Å1£¨”…–˝◊™µƒ–‘÷ µ√°œEDG=90°„£¨Ω”◊≈÷§√˜Rt°˜EDF°◊Rt°˜DGH£¨¿˚”√œýÀ∆µƒ–‘÷ µ√![]() £¨∑÷
£¨∑÷![]() 2∫Õ
2∫Õ![]() £¨¡–∑Ω≥ëÛ≥ˆtµƒ÷µ£¨Ω¯∂¯«Û≥ˆGµƒ◊¯±Í£ª¢⁄µ±µ„G‘⁄∂‘≥∆÷·◊Û≤ýµƒ≈◊ŒÔœþ…œ ±£¨”√Õ¨—˘µƒ∑Ω∑®ø…µ√Gµ„◊¯±Í£Æ
£¨¡–∑Ω≥ëÛ≥ˆtµƒ÷µ£¨Ω¯∂¯«Û≥ˆGµƒ◊¯±Í£ª¢⁄µ±µ„G‘⁄∂‘≥∆÷·◊Û≤ýµƒ≈◊ŒÔœþ…œ ±£¨”√Õ¨—˘µƒ∑Ω∑®ø…µ√Gµ„◊¯±Í£Æ
£®1£©µ±y=0 ±£¨x2©Å2x©Å3=0£¨Ω‚µ√£∫x1=©Å1£¨x2=3£¨‘ÚA£®©Å1£¨0£©£¨B£®3£¨0£©£¨À˘“‘≈◊ŒÔœþµƒ∂‘≥∆÷·Œ™÷±œþx=1£¨µ±x=0 ±£¨y=x2©Å2x©Å3=©Å3£¨‘ÚC£®0£¨©Å3£©£Æ
…Ë÷±œþBCµƒΩ‚Œˆ ΩŒ™y=kx+b£¨∞—B£®3£¨0£©£¨C£®0£¨©Å3£©¥˙»Îµ√£∫![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫![]() £¨À˘“‘÷±œþBCµƒΩ‚Œˆ ΩŒ™y=x©Å3£ª
£¨À˘“‘÷±œþBCµƒΩ‚Œˆ ΩŒ™y=x©Å3£ª
µ±x=1 ±£¨y=x©Å3=1©Å3=£≠2£¨‘ÚDµ„◊¯±ÍŒ™£®1£¨©Å2£©£ª
£®2£©»ÁÕº1£Æ
°þB£®3£¨0£©£¨C£®0£¨©Å3£©£¨°ý°˜OBCŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨°ý°œOCB=°œOBC=45°„£Æ
°þD£®1£¨©Å2£©£¨°ýCD![]() £¨µ±°œEDB=90°„ ±£¨‘Ú°˜CDEŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨°ýCE
£¨µ±°œEDB=90°„ ±£¨‘Ú°˜CDEŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨°ýCE![]() CD
CD![]() 2£¨°ýOE=3©Å2=1£¨¥À ±E£®0£¨©Å1£©£¨°ýµ±m£º©Å1«“m°Ÿ©Å3 ±£¨°œEDBŒ™∂€Ω«£¨°˜EDBŒ™∂€Ω«»˝Ω«–Œ£ª
2£¨°ýOE=3©Å2=1£¨¥À ±E£®0£¨©Å1£©£¨°ýµ±m£º©Å1«“m°Ÿ©Å3 ±£¨°œEDBŒ™∂€Ω«£¨°˜EDBŒ™∂€Ω«»˝Ω«–Œ£ª
µ±°œEBD=90°„ ±£¨‘Ú°˜OBEŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨°ýOE=OB=3£¨¥À ±E£®0£¨3£©£¨°ýµ±m£æ3 ±£¨°œEDBŒ™∂€Ω«£¨°˜EDBŒ™∂€Ω«»˝Ω«–Œ£ª
°ýmµƒ»°÷µ∑∂ŒßŒ™m£æ3ªÚm£º©Å1«“m°Ÿ©Å3£ª
£®3£©¥Ê‘⁄£Æ
¢Ÿµ±µ„G‘⁄∂‘≥∆÷·”“≤ýµƒ≈◊ŒÔœþ…œ ±£¨»ÁÕº2£¨◊˜DF°Õy÷·”⁄F£¨GH°ÕDF”⁄H£¨…ËG£®t£¨t2©Å2t©Å3£©£¨‘ÚGH=t2©Å2t©Å3©Å£®©Å2£©=t2©Å2t©Å1£Æ
°þ…‰œþDE»∆µ„DÀ≥ ±’Î∑ΩœÚ–˝◊™90°„£¨”Î≈◊ŒÔœþΩªµ„Œ™G£¨°ý°œEDG=90°„£¨°ý°œEDF+°œGDH=90°„£¨∂¯°œEDF+°œDEF=90°„£¨°ý°œDEF=°œGDH£¨°ýRt°˜EDF°◊Rt°˜DGH£¨°ý![]() £¨∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫
£¨∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫
i£©»Ù![]() 2£¨‘Ú
2£¨‘Ú![]() 2£¨º¥t2©Å2t©Å1
2£¨º¥t2©Å2t©Å1![]() £¨Ω‚µ√£∫t1=1
£¨Ω‚µ√£∫t1=1![]() £®…·»•£©£¨t2=1
£®…·»•£©£¨t2=1![]() £¨¥À ±Gµ„◊¯±ÍŒ™£®1
£¨¥À ±Gµ„◊¯±ÍŒ™£®1![]() £©£ª
£©£ª
ii£©»Ù![]() £¨‘Ú
£¨‘Ú![]() £¨º¥t2©Å2t©Å1=2£¨Ω‚µ√£∫t1=©Å1£®…·»•£©£¨t2=3£¨¥À ±Gµ„◊¯±ÍŒ™£®3£¨0£©£ª
£¨º¥t2©Å2t©Å1=2£¨Ω‚µ√£∫t1=©Å1£®…·»•£©£¨t2=3£¨¥À ±Gµ„◊¯±ÍŒ™£®3£¨0£©£ª
¢⁄µ±µ„G‘⁄∂‘≥∆÷·◊Û≤ýµƒ≈◊ŒÔœþ…œ ±£¨”√Õ¨—˘µƒ∑Ω∑®ø…µ√Gµ„◊¯±ÍŒ™£®1![]() £©ªÚ£®©Å1£¨0£©£Æ
£©ªÚ£®©Å1£¨0£©£Æ
◊€…œÀ˘ ˆ£∫Gµ„◊¯±ÍŒ™£®1![]() £©ªÚ£®3£¨0£©ªÚ£®1
£©ªÚ£®3£¨0£©ªÚ£®1![]() £©ªÚ£®©Å1£¨0£©£Æ
£©ªÚ£®©Å1£¨0£©£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
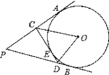
°æƒø°ø»ÁÕº£¨PA°¢PB «°—Oµƒ«–œþ£¨CD«–°—O”⁄µ„E£¨°˜PCDµƒ÷Ð≥§Œ™12£¨°œAPB=60°„£Æ
«Û£∫£®1£©PAµƒ≥§£ª
£®2£©°œCODµƒ∂» ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
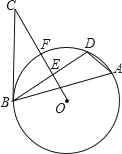
°æƒø°ø»ÁÕº£¨°˜ABD «°—Oµƒƒ⁄Ω”»˝Ω«–Œ£¨E «œ“BDµƒ÷–µ„£¨µ„C «°—OÕ‚“ªµ„«“°œDBC=°œA£¨¡¨Ω”OE—”≥§”Α≤œýΩª”⁄µ„F£¨”ÎBCœýΩª”⁄µ„C£Æ
£®1£©«Û÷§£∫BC «°—Oµƒ«–œþ£ª
£®2£©»Ù°—Oµƒ∞Îæ∂Œ™6£¨BC=8£¨«Ûœ“BDµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
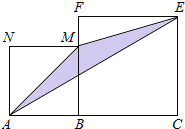
°æƒø°ø»ÁÕº£¨œþ∂ŒAC=n+1£®∆‰÷–nŒ™’˝’˚ ˝£©£¨µ„B‘⁄œþ∂ŒAC…œ£¨‘⁄œþ∂ŒACÕ¨≤ý◊˜’˝∑Ω–ŒABMNº∞’˝∑Ω–ŒBCEF£¨¡¨Ω”AM°¢ME°¢EAµ√µΩ°˜AME£Æµ±AB=1 ±£¨°˜AMEµƒ√ʪ˝º«Œ™S1£ªµ±AB=2 ±£¨°˜AMEµƒ√ʪ˝º«Œ™S2£ªµ±AB=3 ±£¨°˜AMEµƒ√ʪ˝º«Œ™
S3£ª‘ÚS3©ÅS2= £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø6‘¬14»’ «°∞ ¿ΩÁœ◊—™»’°±£¨ƒ≥ –≤…»°◊‘‘∏±®√˚µƒ∑Ω Ω◊È÷Ø –√ғŒҜ◊—™£Æœ◊—™ ±“™∂‘œ◊—™’þµƒ—™–ÕΩ¯––ºÏ≤‚£¨ºÏ≤‚Ω·π˚”–°∞A–Õ°±°¢°∞B–Õ°±°¢°∞AB–Õ°±°¢°∞O–Õ°±4÷÷¿ý–գƑ⁄œ◊—™’þ»À»∫÷–£¨Àʪ˙≥È»°¡À≤ø∑÷œ◊—™’þµƒ—™–ÕΩ·π˚Ω¯––Õ≥º∆£¨≤¢∏˘æð’‚∏ˆÕ≥º∆Ω·π˚÷∆◊˜¡À¡Ω∑˘≤ªÕÍ’˚µƒÕº±Ì£∫
—™–Õ | A | B | AB | O |
»À ˝ | °° °° | 10 | 5 | °° °° |
£®1£©’‚¥ŒÀʪ˙≥È»°µƒœ◊—™’þ»À ˝Œ™°° °°»À£¨m=°° °°£ª
£®2£©≤π»´…œ±Ì÷–µƒ ˝æð£ª
£®3£©»Ù’‚¥ŒªÓ∂Ø÷–∏√ –”–3000»À“ŒҜ◊—™£¨«Îƒ„∏˘æð≥È—˘Ω·π˚ªÿ¥£∫
¥”œ◊—™’þ»À»∫÷–»Œ≥È»°“ª»À£¨∆‰—™–Õ «A–Õµƒ∏≈¬ «∂ý…Ÿ£ø≤¢π¿º∆’‚3000»À÷–¥Û‘º”–∂ý…Ÿ»À «A–Õ—™£ø

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
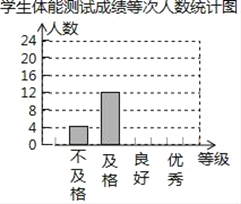
°æƒø°øƒ≥–£Œ™¡ÀΩ‚—ß…˙ÃÂ÷ «Èøˆ£¨¥”∏˜ƒÍº∂Àʪ˙≥È»°≤ø∑÷—ß…˙Ω¯––ÃÐ≤‚ ‘£¨√ø∏ˆ—ß…˙µƒ≤‚ ‘≥…º®∞¥±Í◊º∂‘”¶Œ™”≈–„°¢¡º∫√°¢º∞∏Ò°¢≤ªº∞∏ÒÀƒ∏ˆµ»º∂£¨Õ≥º∆‘±‘⁄Ω´≤‚ ‘ ˝æðªÊ÷∆≥…Õº±Ì ±∑¢œ÷£¨”≈–„¬©Õ≥º∆4»À£¨¡º∫√¬©Õ≥º∆6»À£¨”⁄ «º∞ ±∏¸’˝£¨¥”∂¯–Œ≥…»ÁÕºÕº±Ì£¨«Î∞¥’˝»∑ ˝æðΩ‚¥œ¬¡–∏˜Ã‚£∫
—ß…˙ÃÐ≤‚ ‘≥…º®∏˜µ»¥Œ»À ˝Õ≥º∆±Ì
Ãƒе»º∂ | µ˜’˚«∞»À ˝ | µ˜’˚∫Û»À ˝ |
”≈–„ | 8 | °° °° |
¡º∫√ | 16 | °° °° |
º∞∏Ò | 12 | °° °° |
≤ªº∞∏Ò | 4 | °° °° |
∫œº∆ | 40 | °° °° |
£®1£©ÃÓ–¥Õ≥º∆±Ì£ª
£®2£©∏˘æ𵘒˚∫Û ˝æð£¨≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©»Ù∏√–£π≤”–—ß…˙1500»À£¨«Îƒ„π¿À„≥ˆ∏√–£ÃƒÐ≤‚ ‘µ»º∂Œ™°∞”≈–„°±µƒ»À ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ“–£µ⁄∂˛øŒÃ√ø™’π∫Û ÐµΩ¡À—ß…˙µƒ◊∑≈ı£¨—ß∆⁄Ω· ¯∫Û∂‘≤ø∑÷—ß…˙◊ˆ¡À“ª¥Œ°∞Œ“◊Óœ≤∞Ƶƒµ⁄∂˛øŒÃ√°±Œ æ̵˜≤È£®√ø√˚—ß…˙∂ºÃÓ¡Àµ˜ñÀ±Ì£¨«“÷ª—°¡À“ª∏ˆœÓƒø£©£¨Õ≥º∆∫Û»§Œ∂ ˝—ß°¢—ðΩ≤”Îø⁄≤≈°¢–≈œ¢ºº ı°¢ ÷π§÷∆◊˜∞Ò…œ”–√˚£Æ∆‰÷–—°–≈œ¢ºº ıµƒ»À ˝±»—° ÷π§÷∆◊˜µƒ…Ÿ8»À£ª—°»§Œ∂ ˝—ßµƒ»À ˝≤ªΩˆ±»—° ÷π§÷∆◊˜µƒ»À∂ý£¨«“Œ™’˚ ˝±∂£ª—°»§Œ∂ ˝—ߔΗ° ÷π§÷∆◊˜µƒ»À ˝÷Æ∫Õ «—°—ðΩ≤”Îø⁄≤≈”Η°–≈œ¢ºº ıµƒ»À ˝÷Æ∫Õµƒ5±∂£ª—°»§Œ∂ ˝—ߔΗ°—ðΩ≤”Îø⁄≤≈µƒ»À ˝÷Æ∫Õ±»—°–≈œ¢ºº ı”Η° ÷π§÷∆◊˜µƒ»À ˝÷Æ∫Õ∂ý24»À£Æ‘Ú≤Œº”µ˜≤ÈŒ æ̵ƒ—ß…˙”–________»À°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®±æ¬˙∑÷5∑÷£©»ÁÕº£¨–°√˜‘⁄¥Û¬•30√◊∏þ
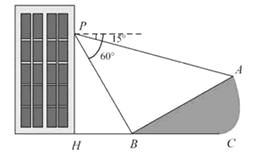
£®º¥PH£Ω30√◊£©µƒ¥∞ø⁄P¥¶Ω¯––π€≤‚£¨≤‚µ√…Ω
∆¬…œA¥¶µƒ∏©Ω«Œ™15°„£¨…ΩΩ≈B¥¶µƒ∏©Ω«Œ™
60°„£¨“—÷™∏√…Ω∆¬µƒ∆¬∂»i£®º¥tan°œABC£©Œ™1£∫
![]() £¨µ„P°¢H°¢B°¢C°¢A‘⁄Õ¨“ª∏ˆ∆Ω√Ê…œ£Æµ„
£¨µ„P°¢H°¢B°¢C°¢A‘⁄Õ¨“ª∏ˆ∆Ω√Ê…œ£Æµ„
H°¢B°¢C‘⁄Õ¨“ªÃı÷±œþ…œ£¨«“PH°ÕHC£Æ
(1)…Ω∆¬∆¬Ω«£®º¥°œABC£©µƒ∂» ˝µ»”⁄ °¯ ∂»£ª
(2)«ÛA°¢B¡Ωµ„º‰µƒæý¿Î£®Ω·π˚æ´»∑µΩ0.1√◊£¨≤Œøº ˝æð£∫![]() °÷1.732£©£Æ
°÷1.732£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°˜ABC÷–£¨D «BCµƒ÷–µ„£¨π˝Dµ„µƒ÷±œþGFΩªAC”⁄F£¨ΩªACµƒ∆Ω––œþBG”⁄Gµ„£¨DE°ÕDF£¨ΩªAB”⁄µ„E£¨¡¨Ω·EG°¢EF£Æ

£®1£©«Û÷§£∫BG£ΩCF£Æ
£®2£©«Îƒ„≈–∂œBE+CF”ÎEFµƒ¥Û–°πÿœµ£¨≤¢Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com