
分析 结合二次函数图象的开口方向、对称轴以及增减性进行解答即可.
解答 解:二次函数y=-(x-1)2+5的大致图象如下: .
.
①当m≤0≤x≤n<1时,当x=m时y取最小值,即2m=-(m-1)2+5,
解得:m=-2.
当x=n时y取最大值,即2n=-(n-1)2+5,
解得:n=2或n=-2(均不合题意,舍去);
②当m≤0≤x≤1≤n时,当x=m时y取最小值,即2m=-(m-1)2+5,
解得:m=-2.
当x=1时y取最大值,即2n=-(1-1)2+5,
解得:n=$\frac{5}{2}$,
所以m+n=-2+$\frac{5}{2}$=$\frac{1}{2}$.
点评 本题考查了二次函数的最值问题,二次函数的增减性,根据函数解析式求出对称轴解析式是解题的关键.


科目:初中数学 来源: 题型:选择题
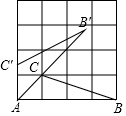 如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )
如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )| A. | $\frac{π}{2}$ | B. | π | C. | 6π | D. | 7π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
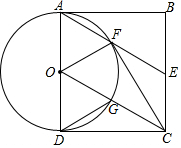 如图,正方形ABCD,E为BC边的中点,连接AE、OC,以AD为直径的⊙O交AE于点F,交OC于点G,连接CF,DG.
如图,正方形ABCD,E为BC边的中点,连接AE、OC,以AD为直径的⊙O交AE于点F,交OC于点G,连接CF,DG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
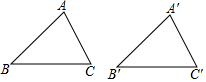 ①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.
①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com