
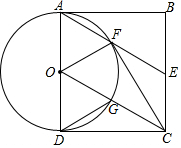
 如图,正方形ABCD,E为BC边的中点,连接AE、OC,以AD为直径的⊙O交AE于点F,交OC于点G,连接CF,DG.
如图,正方形ABCD,E为BC边的中点,连接AE、OC,以AD为直径的⊙O交AE于点F,交OC于点G,连接CF,DG.分析 (1)只要证明△ODC≌△OFC(SAS),即可推出∠OFC=∠ODC=90°,解决问题.
(2)如图2中,作GH⊥CD于H.设OA=OD=a,则CD=2a.在Rt△OCD中,OC=$\sqrt{C{D}^{2}+O{D}^{2}}$=$\sqrt{5}$a,推出CG=($\sqrt{5}$-1)a,由GH∥OD,推出$\frac{GH}{OD}$=$\frac{CG}{CO}$=$\frac{CH}{CD}$,求出GH、DH即可解决问题.
解答 解:(1)证明:如图1,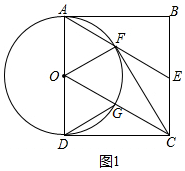
∵四边形ABCD是正方形,
∴AD∥BC,AD=BC,∠ADC=90°,
∵E为BC边中点,AO=DO
∴AO=$\frac{1}{2}$AD,EC=$\frac{1}{2}$BC,
∴AO=EC,AO∥EC,
∴四边形OAEC是平行四边形,
∴AE∥OC,
∴∠DOC=∠OAF,
∠FOC=∠OFA,
∵OA=OF,
∴∠OAF=∠OFA,
∴∠DOC=∠FOC,
在△ODC与△OFC中,
$\left\{\begin{array}{l}{OD=OF}\\{∠DOC=∠FOC}\\{OC=OC}\end{array}\right.$,
∴△ODC≌△OFC(SAS),
∴∠OFC=∠ODC=90°,
∴OF⊥CF,
∴CF与⊙O相切;
(2)如图2中,作GH⊥CD于H.设OA=OD=a,则CD=2a.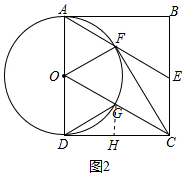
在Rt△OCD中,OC=$\sqrt{C{D}^{2}+O{D}^{2}}$=$\sqrt{5}$a,
∴CG=($\sqrt{5}$-1)a,
∵GH∥OD,
∴$\frac{GH}{OD}$=$\frac{CG}{CO}$=$\frac{CH}{CD}$,
∴$\frac{GH}{a}$=$\frac{(\sqrt{5}-1)a}{\sqrt{5}a}$=$\frac{CH}{2a}$,
∴GH=$\frac{\sqrt{5}-1}{\sqrt{5}}$a,CH=$\frac{\sqrt{5}-1}{2\sqrt{5}}$a,
∴DH=2a-$\frac{\sqrt{5}-1}{2\sqrt{5}}$a,
∴tan∠GDC=$\frac{GH}{DH}$=$\frac{\frac{\sqrt{5}-1}{\sqrt{5}}a}{2a-\frac{\sqrt{5}-1}{2\sqrt{5}}a}$=$\frac{8-2\sqrt{5}}{11}$.
点评 此题主要考查了全等三角形的判定与性质以及勾股定理和平行四边形的判定、切线的判定等知识,得出△ODC≌△OFC是解题关键,学会添加常用辅助线,属于中考常考题型.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
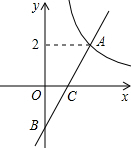 已知,在平面直角坐标系xOy中,函数y=$\frac{4}{x}$(x>0)的图象与一次函数y=kx-k的图象的交点为A(m,2).
已知,在平面直角坐标系xOy中,函数y=$\frac{4}{x}$(x>0)的图象与一次函数y=kx-k的图象的交点为A(m,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一个数阵,每行和每列元素个数都是无限的,但是我们可以按照以下规律,将每个元素都标序(以下右边是数阵中的元素,左边是其序号):1←→a${\;}_{1}^{1}$,2←→a${\;}_{2}^{1}$,3←→a${\;}_{1}^{2}$,4←→a${\;}_{3}^{1}$,5←→a${\;}_{2}^{2}$,6←→a${\;}_{1}^{3}$,7←→a${\;}_{4}^{1}$,…,11←→a${\;}_{5}^{1}$,…,按此规律填写下列空格:18←→${a}_{3}^{3}$,80←→a${\;}_{12}^{2}$.
如图,一个数阵,每行和每列元素个数都是无限的,但是我们可以按照以下规律,将每个元素都标序(以下右边是数阵中的元素,左边是其序号):1←→a${\;}_{1}^{1}$,2←→a${\;}_{2}^{1}$,3←→a${\;}_{1}^{2}$,4←→a${\;}_{3}^{1}$,5←→a${\;}_{2}^{2}$,6←→a${\;}_{1}^{3}$,7←→a${\;}_{4}^{1}$,…,11←→a${\;}_{5}^{1}$,…,按此规律填写下列空格:18←→${a}_{3}^{3}$,80←→a${\;}_{12}^{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com