【题目】解下面各题
（1）解方程：x2﹣4x﹣12=0；
（2）解不等式组：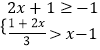 
．
【答案】
（1）解：（x﹣6）（x+2）=0，
x﹣6=0或x+2=0，
所以x1=6，x2=﹣2；
（2）解：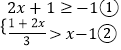 
解①得x≥﹣1，
解②得x＜4，
所以不等式组的解集是﹣1≤x＜4．
【解析】（1）利用因式分解法解方程；（2）分别解两个不等式得到x≥﹣1和x＜4，然后根据大小小大中间找确定不等式组的解集．
【考点精析】本题主要考查了一元一次不等式组的解法的相关知识点，需要掌握解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题．
科目：初中数学 来源： 题型：
【题目】如图，已知OA⊥OB，∠AOD=∠BOC由此判定OC⊥OD，下面是推理过程，请填空.
解：∵OA⊥OB(已知)
所以_____=90°（________）
因为_____=∠AOD-∠AOC，____=∠BOC-∠AOC，∠AOD=∠BOC，
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
科目：初中数学 来源： 题型：
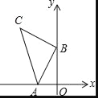
【题目】如图，在平面直角坐标系中，点A的坐标为（﹣2，0），点B的坐标为（0，n），以点B为直角顶点，点C在第二象限内，作等腰直角△ABC．则点C的坐标是_____（用字母n表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线l与⊙O相离，OA⊥l于点A，交⊙O于点P，点B是⊙O上一点，连接BP并延长，交直线l于点C，使得AB=AC．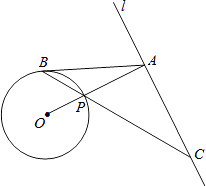 
（1）求证：AB是⊙O的切线；
（2）PC=2 
，OA=4． ①求⊙O的半径；
②求线段PB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)…按这样的运动规律,经过第2015次运动后,动点P的坐标是____.
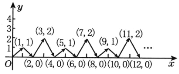
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，AD平分∠BAC，DE⊥AB，DF⊥AC，E、F分别为垂足，则下列四个结论：①∠DEF=∠DFE； ②AE=AF； ③AD平分∠EDF； ④AD垂直平分EF.其中正确结论有（）
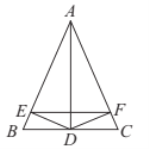
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
（1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE= 度；
（2）设∠BAC= 
，∠DCE= 
．
① 如图2，当点D在线段CB上，∠BAC≠90°时，请你探究
与
之间的数量关系，并证明你的结论；
② 如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，并直接写出此时
与
之间的数量关系（不需证明）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在锐角△ABC中，∠ABC=45°，高线AD、BE相交于点F．
（1）判断BF与AC的数量关系并说明理由；
（2）如图2，将△ACD沿线段AD对折，点C落在BD上的点M，AM与BE相交于点N，当DE∥AM时，判断NE与AC的数量关系并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“数形结合"是一种重要的数学思想，观察下面的图形和算式.
解答下列问题：
(1)试猜想1+3+5+7+9+…+19=______=（ ）；
(2)试猜想，当n是正整数时，1+3+5+7+9+…+(2n-1)= ；
(3)请用（2）中得到的规律计算：19+21+23+25+27+…+99.
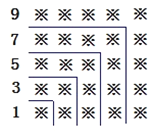
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com