
【题目】如图,在△ABC中,∠ACB=90°,AC=30cm,BC=40cm.点P从点A出发,以5cm/s的速度沿AC向终点C匀速移动.过点P作PQ⊥AB,垂足为点Q,以PQ为边作正方形PQMN,点M在AB边上,连接CN.设点P移动的时间为t(s).

(1)PQ=______;(用含t的代数式表示)
(2)当点N分别满足下列条件时,求出相应的t的值;①点C,N,M在同一条直线上;②点N落在BC边上;
(3)当△PCN为等腰三角形时,求t的值.
【答案】(1)4t;(2)①![]() ,②
,②![]() ;(3)
;(3)![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)先求出AB=50,sinA=![]() =
=![]() ,cosA=
,cosA=![]() =
=![]() ,进而求出AQ=3t,PQ=4t,即可得出结论;
,进而求出AQ=3t,PQ=4t,即可得出结论;
(2)先判断出PN=QM=PQ=4t,
①求出CD=24,AD=18,进而判断出AQ+QM=AD=18,建立方程即可得出结论;
②判断出∠APQ=∠PNC,进而得出△AQP∽△PCN,建立方程即可得出结论;
(3)分三种情况,利用等腰三角形的性质建立方程求解即可得出结论.
解:(1)在Rt△ABC中,根据勾股定理得,AB=50,
∴sinA=![]() =
=![]() ,cosA=
,cosA=![]() =
=![]()
∵PQ⊥AB,
∴∠AQP=90°,
由运动知,AP=5t,
在Rt△AQP中,AQ=APcosA=![]() ×5=3t,PQ=APsinA=4t,
×5=3t,PQ=APsinA=4t,
故答案为:4t;
(2)由(1)知,AQ=3t,PQ=4t,
∵四边形PQMN是正方形,
∴PN=QM=PQ=4t,
①如图1,
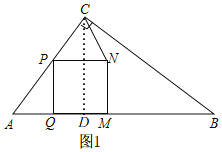
由(1)知,AB=50,
过点C作CD⊥AB于D,
∴![]() ABCD=
ABCD=![]() ACBC,
ACBC,
∴CD=24,
在Rt△ADQ中,AD=![]() =18,
=18,
∵点C,N,M在同一条直线上,
∴点M落在点D,
∴AQ+QM=AD=18,
由(1)知,QM=PQ=4t,AQ=3t,
∴4t+3t=18,
∴t=![]() ;
;
②点N落在BC上时,∠PCN=∠PCB=90°=∠AQP,
∴∠CPN+∠CNP=90°,
∵∠QPN=90°
∴∠CPN+∠APQ=90°,
∴∠APQ=∠PNC,
∵∠AQP=∠PCN,
∴△AQP∽△PCN,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ;
;
(3)当PC=PN时,30-5t=4t,
∴t=![]() ,
,
当PC=NC时,如图2,过点C作CF⊥PN于F,延长CF交AB于D,
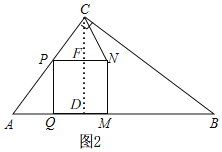
∴PF=![]() PN=2t,
PN=2t,
∴QD=2t,
根据勾股定理得,AQ=![]() =3t,
=3t,
∴AD=AQ+QD=5t=18,
∴t=![]() ,
,
当PN=NC时,如图3,过点N作NG⊥AC于G,
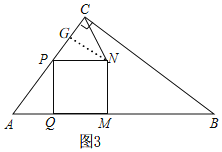
∴PG=![]() PC=
PC=![]() ,
,
易知,△PNG∽△APQ,
∴![]() ,
,
∴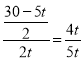 ,
,
∴t=![]() ,
,
即:当△PCN是等腰三角形时,![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
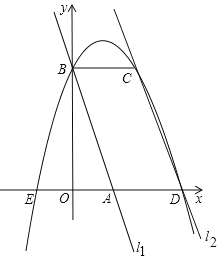
【题目】如图,在平面直角坐标系中两条直线为l1:y=–3x+3,l2:y=–3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中:
①a–b+c=0;
②2a+b+c=5;
③抛物线关于直线x=1对称;
④抛物线过点(b,c);
⑤S四边形ABCD=5;
其中正确的个数有( )
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距180km.新修的高速公路开通后,从A地到B地的长途客车的平均速度提高了50%,行驶时间缩短了1h.请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
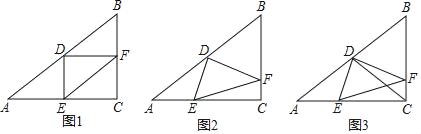
【题目】如图,已知△ABC中,∠ACB=90°,AC=8,cosA=![]() ,D是AB边的中点,E是AC边上一点,联结DE,过点D作DF⊥DE交BC边于点F,联结EF.
,D是AB边的中点,E是AC边上一点,联结DE,过点D作DF⊥DE交BC边于点F,联结EF.
(1)如图1,当DE⊥AC时,求EF的长;
(2)如图2,当点E在AC边上移动时,∠DFE的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出∠DFE的正切值;
(3)如图3,联结CD交EF于点Q,当△CQF是等腰三角形时,请直接写出BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
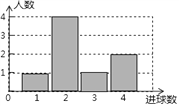
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.

(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com