【题目】已知:x=2
+1,y=-1，
求:（1）
的立方根；（2）
的平方根；（3）
的值
【答案】（1）立方根为3；（2）平方根为±3
；（3）7．
【解析】
（1）根据完全平方公式得到x2+2xy+y2=（x+y）2，再代入计算，进一步根据立方根的定义求解即可；
（2）先代入求出x2+y2-2
+1的值，进一步求得平方根；
（3）将x=2+1，y=-1代入（4+2）y2+（2-1）x-8，再根据完全平方公式和平方差公式求值即可．
解：（1）∵x=2+1，y=-1，
∴x2+2xy+y2
=（x+y）2
=（2+1+-1）2
=27，
27的立方根为3；
（2）∵x=2+1，y=-1，
∴x2+y2-2+1
=（2+1）2+（-1）2-2+1
=13+4+4-2-2+1
=18，
18的平方根为±3 ；
（3）∵x=2+1，y=-1，
∴（4+2）y2+（2-1）x-8
=（4+2）（-1）2+（2-1）（2+1）-8
=（4+2）（4-2）+12-1-8
=16-12+12-1-8
=7．
故答案为：（1）立方根为3；（2）平方根为±3 ；（3）7．
快乐5加2金卷系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB=90°，AC=30cm，BC=40cm．点P从点A出发，以5cm/s的速度沿AC向终点C匀速移动．过点P作PQ⊥AB，垂足为点Q，以PQ为边作正方形PQMN，点M在AB边上，连接CN．设点P移动的时间为t（s）．
（1）PQ=______；（用含t的代数式表示）
（2）当点N分别满足下列条件时，求出相应的t的值；①点C，N，M在同一条直线上；②点N落在BC边上；
（3）当△PCN为等腰三角形时，求t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式，如
就是完全对称式(代数式中
换成b，b换成，代数式保持不变).下列三个代数式：①
；②
；③
．其中是完全对称式的是（ ）
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目：初中数学 来源： 题型：
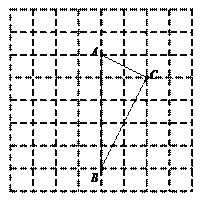
【题目】如图，在由边长为1的小正方形组成的网格图中，有一个格点三角形ABC．（注：顶点均在网格线交点处的三角形称为格点三角形．）
（1）△ABC是 三角形（填“锐角”、“直角”或“钝角”）；
（2）若P、Q分别为线段AB、BC上的动点，当PC＋PQ取得最小值时，
① 在网格中用无刻度的直尺，画出线段PC、PQ．（请保留作图痕迹．）
② 直接写出PC＋PQ的最小值： .
查看答案和解析>>
科目：初中数学 来源： 题型：
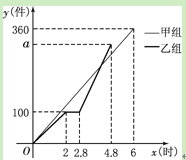
【题目】甲、乙两组工人同时加工某种零件，乙组工作中有一次停产更换设备，更换设备
后，乙组的工作效率是原来的2倍．两组各自加工零件的数量
(件)与时间
(时)的函数图
象如图所示．
（1）求甲组加工零件的数量y与时间
之间的函数关系式．（2分）
（2）求乙组加工零件总量
的值．（3分）
（3）甲、乙两组加工出的零件合在一起装箱，每够300件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？再经过多长时间恰好装满第2箱？（5分）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点E是正方形ABCD的对角线BD上一点，并且AD=DE，过点E作EF⊥BD交AB于点F.
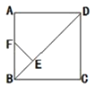
（1）求证：AF=BE,（2）若正方形的边长为1，求BF的长度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】直线y＝kx+k﹣2经过点（m，n+1）和（m+1，2n+3），且﹣2＜k＜0，则n的取值范围是（ ）
A. ﹣2＜n＜0B. ﹣4＜n＜﹣2C. ﹣4＜n＜0D. 0＜n＜﹣2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点E，F在矩形的边AD，BC上，点B与点D关于直线EF对称．设点A关于直线EF的对称点为G．
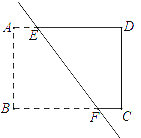
（1）画出四边形ABFE关于直线EF对称的图形；
（2）若∠FDC＝16°，直接写出∠GEF的度数为 ；
（3）若BC＝4，CD＝3，写出求线段EF长的思路．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列叙述中，①所有的正数都是整数；②|a|一定是正数；③无限小数一定是无理数；④(－2)3没有平方根；⑤
的平方根是±2．其中不正确的个数有（ ）
A.2个B.3个C.4个D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com