
如图所示,在Rt ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为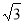 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt ABC顺时针旋转120
ABC顺时针旋转120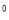 后得到Rt
后得到Rt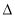 ADE,点B、C的对应点分别是点D、E.
ADE,点B、C的对应点分别是点D、E.
(1)画出旋转后的Rt ADE;
ADE;
(2)求出Rt ADE的直角边DE被⊙M截得的弦PQ的长度;
ADE的直角边DE被⊙M截得的弦PQ的长度;
(3)判断Rt ADE的斜边AD所在的直线与⊙M的位置关系,并说明理由.
ADE的斜边AD所在的直线与⊙M的位置关系,并说明理由.
(1)作图见解析;(2)2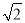 .(3)AD与⊙M相切.理由见解析.
.(3)AD与⊙M相切.理由见解析.
【解析】
试题分析:(1)把三角形ABC绕A旋转120°就能得到图形.
(2)连接MQ,过M点作MF⊥DE,由AN=3,AC=4,求出NE的长;在Rt△MFQ中,利用勾股定理可求出QF,根据垂径定理知QF就是弧长PQ的一半.
(3)过M作AD的垂线设垂足为H,然后证MH与⊙M半径的大小关系即可;连接AM、MN,由于AE是⊙M的切线,故MN⊥AE,在Rt△AMN中,通过解直角三角形,易求得∠MAN=30°,由此可证得AM是∠DAE的角平分线,根据角平分线的性质即可得到MH=MN,由此可证得⊙M与AD相切.
试题解析:(1)如图Rt△ADE就是要画的图形
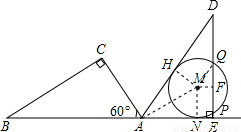
(2)连接MQ,过M点作MF⊥DE,垂足为F,由Rt△ABC可知,NE=1,
在Rt△MFQ中,解得FQ=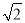 ,故弦PQ的长度2
,故弦PQ的长度2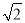 .
.
(3)AD与⊙M相切.
证明:过点M作MH⊥AD于H,连接MN,MA,则MN⊥AE,且MN=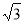 ,
,
在Rt△AMN中,tan∠MAN=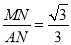 ,
,
∴∠MAN=30°,
∵∠DAE=∠BAC=60°,
∴∠MAD=30°,
∴∠MAN=∠MAD=30°,
∴MH=MN,
∴AD与⊙M相切.
考点:1.切线的判定;2.作图-旋转变换.


科目:初中数学 来源:2014-2015学年四川省仁寿县联谊学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,正方形网格中,ΔABC 的顶点及点 在格点上。
在格点上。

(1)画出与ΔABC 关于点O对称的Δ ;
;
(2)画出一个以点O为位似中心的Δ ,使得Δ
,使得Δ 与 Δ
与 Δ 的位似比为2。
的位似比为2。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省仁寿县联谊学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
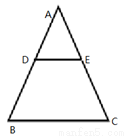
如图,已知DE//BC,AB=14,AC=18,AE=10则AD的长为( )
A.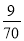 B.
B.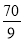 C.
C.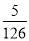 D.
D.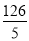
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省仁寿县联谊学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列各组中的四条线段成比例的是( )
A.4cm,2cm,1cm,3cm
B.1cm,2cm,3cm,5cm
C.3cm,4cm,5cm,6cm
D.1cm,2cm,2cm,4cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省九年级上学期第二次月考数学试卷(解析版) 题型:解答题
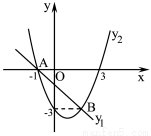
如图,A(-1,0),B(2,-3)两点都在一次函数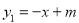 与二次函数
与二次函数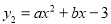 的图象上.
的图象上.
(1)求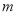 和
和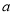 ,
,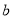 的值;
的值;
(2)请直接写出当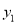 >
>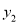 时,自变量
时,自变量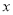 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省九年级上学期第二次月考数学试卷(解析版) 题型:填空题
如下图,△ABC中,∠C=30°.将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC交于F,则∠AFB= °.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省咸宁市九年级上学期第四次月考数学试卷(解析版) 题型:解答题
(12分)已知关于x的方程 .
.
(1)求证:无论m取任何实数时,方程恒有实数根;(3分)
(2)若关于x的二次函数 的图象与x轴两交点间的距离为2时,求抛物线的解析式。(4分)
的图象与x轴两交点间的距离为2时,求抛物线的解析式。(4分)
(3)在同一直角坐标系xOy中,画出(2)中所有函数图象,结合图象回答问题:当直线 与(2)中的这个函数图象只有两个交点时,求b的取值范围。(5分)
与(2)中的这个函数图象只有两个交点时,求b的取值范围。(5分)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com