新辅教导学系列答案
阳光同学一线名师全优好卷系列答案科目：初中数学 来源：2015年初中毕业升学考试（广东茂名卷）数学（解析版） 题型：选择题
（3分）如图，四边形ABCD是⊙O的内接四边形，∠B=70°，则∠D的度数是（ ）
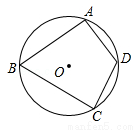
A．110° B．90° C．70° D．50°
查看答案和解析>>
科目：初中数学 来源：2014-2015学年江苏省无锡市江阴市要塞片中考二模数学试卷（解析版） 题型：填空题
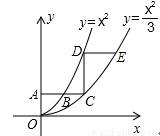
如图，平行于x轴的直线AC分别交抛物线y1=x2（x≥0）与y2=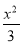
（x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则
= ．
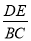查看答案和解析>>
科目：初中数学 来源：2014-2015学年江苏省无锡市崇安区中考一模数学试卷（解析版） 题型：解答题
已知：如图①，在矩形ABCD中，AB=5，AD=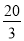
，AE⊥BD，垂足是E．点F是点E关于AB的对称点，连接AF、BF．
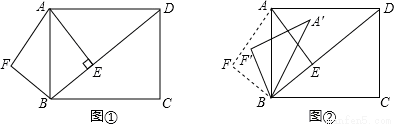
（1）求AE和BE的长；
（2）若将△ABF沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．当点F分别平移到线段AB．AD上时，直接写出相应的m的值．
（3）如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P，与直线BD交于点Q．是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年江苏省无锡市崇安区中考一模数学试卷（解析版） 题型：解答题
如图，正方形ABCD中，点E在对角线AC上，连接EB．ED．
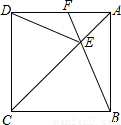
（1）求证：△BCE≌△DCE；
（2）延长BE交AD于点F，若∠DEB=140°，求∠AFE的度数．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年江苏省无锡市崇安区中考一模数学试卷（解析版） 题型：选择题
一次函数y=-2x+4的图象与y轴的交点坐标是（ ）
A．（0，4） B．（4，0） C．（2，0） D．（0，2）
查看答案和解析>>
科目：初中数学 来源：2014-2015学年江苏省南京市建邺区中考一模数学试卷（解析版） 题型：填空题
一组数据4、5、6、7、8的方差为S12，另一组数据3、5、6、7、9的方差为S22，那么S12 S22（填“＞”、“=”或“＜”）．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年浙江省七年级下学期期中考试数学试卷（解析版） 题型：解答题
（本题9分）把代数式通过配凑等手段，得到完全平方式，再运用完全平方式是非负性这一性质增加问题的条件，这种解题方法叫做配方法．配方法在代数式求值，解方程，最值问题等都有着广泛的应用．
例如：①用配方法因式分【解析】
a2+6a+8
原式=a2+6a+9－1
=（a+3）2 –1
=（a+3－1）（a+3+1）
=（a+2）（a+4）
②若M=a2－2ab+2b2－2b+2，利用配方法求M的最小值：
a2－2ab+2b2－2b+2=a2－2ab+b2+b2－2b+1+1
=（a－b）2+（b－1）2 +1
∵（a－b）2≥0，（b－1）2 ≥0
∴当a=b=1时，M有最小值1
请根据上述材料解决下列问题：
（1）在横线上添上一个常数项使之成为完全平方式：a 2+4a+ ．
（2）用配方法因式分解： a2－24a+143
（3）若M=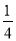
a2+2a +1，求M的最小值．
（4）已知a2+b2+c2－ab－3b－4c+7=0，求a+b+c的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
