
【题目】阅读理解:已知Q、K、R为数轴上三点,若点K到点Q的距离是点K到点R的距离的2倍,我们就称点K是有序点对![]() 的好点.
的好点.
根据下列题意解答问题:
(1)如图1,数轴上点Q表示的数为1,点P表示的数为0,点K表示的数为1,点R表示的数为2.因为点K到点Q的距离是2,点K到点R的距离是1,所以点K是有序点对![]() 的好点,但点K不是有序点对
的好点,但点K不是有序点对![]() 的好点.同理可以判断:点P是不是有序点对
的好点.同理可以判断:点P是不是有序点对![]() 的好点;
的好点;
(2)如图2,数轴上点M表示的数为-1,点N表示的数为5,点H表示的数为x,若点H是有序点对![]() 的好点,求x的值;
的好点,求x的值;
(3)如图3,数轴上点A表示的数为20,点B表示的数为10.现有一只电子蚂蚁C从点B出发,以每秒3个单位的速度向左运动t秒(t>0).当点A、B、C中恰有一个点为其余两有序点对的好点,直接写出t的所有可能的值.

【答案】(1)点P不是有序点对![]() 的好点;(2)11或3;(3)
的好点;(2)11或3;(3)![]() ,5,15,20,30.
,5,15,20,30.
【解析】
(1)根据定义发现:好点表示的数到[Q,R]中,前面的点Q是到后面的数R的距离的2倍,从而得出结论;
(2)点M到点N的距离为6,根据定义得:好点所表示的数为11;
(3)由好点的定义可知:分两种情况列式:①当点C在点A、B之间;②当点A在点C、B之间;可以得出结论.
(1)∵PQ=1,RP=2,∴PQ≠2PR,∴点P不是有序点对[Q,R]的好点.
故答案为:不是;
(2)∵点H是有序点对[M,N]的好点,∴HM=2HN,∴|x-(-1)|=2|x-5| ,即|x+1|=|2x-10| .
①当x+1=2x-10时,解得:x=11;
②当x+1=-(2x-10)时,解得:x=3.
综上所述:x=11或3.
(3)AB=10﹣(﹣20)=30,CB=3t.
当点C在点A、B之间:
①若点C为有序点对[A,B]的好点,则CA=2CB,CB=10,3t=10,解得:t=![]() (秒).
(秒).
②若点C为有序点对[B,A]的好点,即CB=2CA,CB=20,3t=20,解得:t=![]() (秒).
(秒).
③若点B为有序点对[A,C]的好点或点A为有序点对[B,C]的好点,即BA=2BC或AB=2AC,CB=15,3t=15,解得:t=5(秒);
当点A在点C、B之间:
①点A为有序点对[B,C]的好点,即AB=2AC,CB=45,3t=45,解得:t=15(秒).
②点C为有序点对[B,A]的好点或点B为有序点对[C,A]的好点,即CB=2CA或BC=2BA,CB=60,3t=60,解得:t=20(秒);
③点A为有序点对[C,B]的好点,即AC=2AB,CB=90,3t=90,解得:t=30.
综上所述:当经过![]() 秒或
秒或![]() 秒或5秒或15秒或20秒或30秒时,A、B、C中恰有一个点为其余两有序点对的好点.
秒或5秒或15秒或20秒或30秒时,A、B、C中恰有一个点为其余两有序点对的好点.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP.
(1)当m=3时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,问m为何值时CA⊥CP?
(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3∶4∶5∶8∶6,又知此次调查中捐款25元和30元的学生一共42人.

(1)他们一共调查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,估计全校学生捐款多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过调查获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题: 
(1)这次活动一共调查了名学生;
(2)补全条形统计图,并求出扇形统计图中选择篮球项目的人数所在扇形的圆心角的度数;
(3)若该学校有1200人,则该学校选择足球项目的学生人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潮州旅游文化节开幕前,某凤凰茶叶公司预测今年凤凰茶叶能够畅销,就用32000元购进了一批凤凰茶叶,上市后很快脱销,茶叶公司又用68000元购进第二批凤凰茶叶,所购数量是第一批购进数量的2倍,但每千克凤凰茶叶进价多了10元.
(1)该凤凰茶叶公司两次共购进这种凤凰茶叶多少千克?
(2)如果这两批茶叶每千克的售价相同,且全部售完后总利润率不低于20%,那么每千克售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在热气球上A处测得塔顶B的仰角为52°,测得塔底C的俯角为45°,已知A处距地面98米,求塔高BC.(结果精确到0.1米)
【参考数据:sin52°=0.79,cos52°=0.62,tan52°=1.28】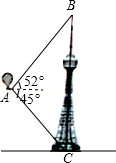
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com