
【题目】(1)3![]() ﹣
﹣![]() ﹣2
﹣2![]()
(2)(2﹣![]() )(2+
)(2+![]() )+(2﹣
)+(2﹣![]() )2﹣
)2﹣![]()
(3)解方程组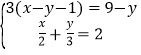
(4)![]()
(5)求x的值:25(x+2)2﹣36=0.
【答案】(1)![]() (2)5-5
(2)5-5![]() (3)
(3)![]() (4)
(4)![]() (5)x1=
(5)x1=![]() ,x2=
,x2=![]()
【解析】
(1)先分别化简,然后再合并同类二次根式即可;
(2)先利用完全平方公式、平方差公式进行展开,然后再合并同类二次根式即可得;
(3)整理后利用加减消元法进行求解即可得;
(4)利用加减消元法进行求解即可得;
(5)移项整理后利用平方根的定义进行求解即可得.
(1)原式=6![]() ﹣
﹣![]() ﹣
﹣![]() =
=![]() ;
;
(2)原式=4﹣5+4﹣4![]() +2﹣
+2﹣![]() =5﹣5
=5﹣5![]() ;
;
(3)方程组整理为![]() ,
,
①+②得6x=24,解得x=4,
把x=4代入②得12+2y=12,解得y=0,
所以方程组的解为![]() ;
;
(4)![]() ,
,
①×3﹣②×2得9y﹣8y=36﹣34,
解得y=2,
把y=2代入①得2x+6=12,解得x=3,
所以方程组的解为![]() ;
;
(5)(x﹣2)2=![]() ,
,
x﹣2=±![]() ,
,
所以x1=![]() ,x2=
,x2=![]() .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中∠C=90°,点O是AB边上一点,以OA为半径作⊙O,与边AC交于点D,连接BD,若∠DBC=∠A,求证:BD是⊙O的切线. 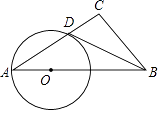
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:已知Q、K、R为数轴上三点,若点K到点Q的距离是点K到点R的距离的2倍,我们就称点K是有序点对![]() 的好点.
的好点.
根据下列题意解答问题:
(1)如图1,数轴上点Q表示的数为1,点P表示的数为0,点K表示的数为1,点R表示的数为2.因为点K到点Q的距离是2,点K到点R的距离是1,所以点K是有序点对![]() 的好点,但点K不是有序点对
的好点,但点K不是有序点对![]() 的好点.同理可以判断:点P是不是有序点对
的好点.同理可以判断:点P是不是有序点对![]() 的好点;
的好点;
(2)如图2,数轴上点M表示的数为-1,点N表示的数为5,点H表示的数为x,若点H是有序点对![]() 的好点,求x的值;
的好点,求x的值;
(3)如图3,数轴上点A表示的数为20,点B表示的数为10.现有一只电子蚂蚁C从点B出发,以每秒3个单位的速度向左运动t秒(t>0).当点A、B、C中恰有一个点为其余两有序点对的好点,直接写出t的所有可能的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了顺利通过“国家文明城市”验收,市政府拟对部分路段的人行道地砖、绿化带、排水管等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完成工程,又能使工程费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,∠ABC的角平分线BE将边AD分成长度为5cm和6cm的两部分,则平行四边形ABCD的周长为__________________cm.
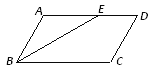
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)若我市初中生共有16000人,竞赛活动获奖率为40%,获三等奖以上的学生表示对“足球比较喜欢”,请你估计我市初中生对“足球比较喜欢”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com