
【题目】在下列条件中:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A=∠B=a∠C;④∠A∶∠B∶∠C=1∶2∶3,能确定△ABC为直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
根据所给的4个条件分别求出4个条件下△ABC中的最大角的度数,再进行判断即可.
①∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴∠C=180°×![]() =90°,
=90°,
∴此时△ABC是直角三角形;
②∵∠A=∠B=2∠C,∠A+∠B+∠C=180°,
∴5∠C=180°,解得∠C=36°,
∴∠A=∠B=72°,
∴此时△ABC不是直角三角形;
③∵∠A=∠B=a∠C,∠A+∠B+∠C=180°,
∴(2a+1)∠C=180°,解得∠C=![]() ,
,
∴∠A=∠B=![]() ,
,
∴此时△ABC中三个内角的度数是不确定的,
∴不能确定△ABC是否是直角三角形;
④∵∠A∶∠B∶∠C=1∶2∶3,∠A+∠B+∠C=180°,
∴∠C=180°×![]() =90°,
=90°,
∴此时△ABC是直角三角形.
综上所述,根据上述条件能够确定△ABC是直角三角形的有2个.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE. 
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F. (Ⅰ)试判断直线BC与⊙O的位置关系,并说明理由;
(Ⅱ)若BD=2 ![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).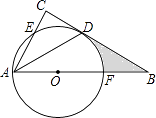
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)当∠BAD=60°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=10,BC=8,P为AD上一点,将△ABP沿BP翻折至△EBP(点A落在点E处),PE与CD相交于点O,且OE=OD,则DP的长为( )

A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.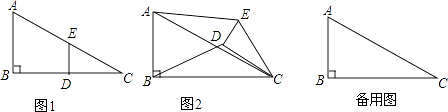
(1)问题发现
①当α=0°时, ![]() =;②当α=180°时,
=;②当α=180°时, ![]() = .
= .
(2)拓展探究
试判断:当0°≤α<360°时, ![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com