
【题目】如图,在ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则 ![]() 的长为 .
的长为 . 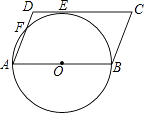
【答案】π
【解析】解:如图连接OE、OF, 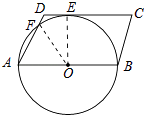
∵CD是⊙O的切线,
∴OE⊥CD,
∴∠OED=90°,
∵四边形ABCD是平行四边形,∠C=60°,
∴∠A=∠C=60°,∠D=120°,
∵OA=OF,
∴∠A=∠OFA=60°,
∴∠DFO=120°,
∴∠EOF=360°﹣∠D﹣∠DFO﹣∠DEO=30°,![]() 的长=
的长= ![]() =π.
=π.
所以答案是:π.
【考点精析】掌握平行四边形的性质和切线的性质定理是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图甲是任意一个直角三角形ABC,它的两条直角边的长分别为a,b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.
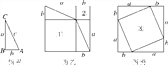
(1)图乙、图丙中①②③都是正方形.由图可知:①是以________为边长的正方形,②是以________为边长的正方形,③是以________为边长的正方形;
(2)图乙中①的面积为________,②的面积为________,图丙中③的面积为________;
(3)图乙中①②面积之和为__________;
(4)图乙中①②的面积之和与图丙中正方形③的面积有什么关系?为什么?由此你能得到关于直角三角形三边长的关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细心观察下图,认真分析各式,然后解答问题.
(![]() )2+1=2,S1=
)2+1=2,S1=![]() ;
;
(![]() )2+1=3,S2=
)2+1=3,S2=![]() ;
;
(![]() )2+1=4,S3=
)2+1=4,S3=![]() .
.
(1)请用含n(n是正整数)的等式表示上述式子的变化规律;
(2)推算出OA10的长;
(3)求出S12+S22+S32+…+S102的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4). (Ⅰ)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(Ⅱ)以点O为位似中心,将△ABC缩小为原来的 ![]() ,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.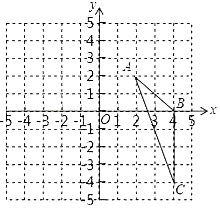
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A=∠B=a∠C;④∠A∶∠B∶∠C=1∶2∶3,能确定△ABC为直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 ()元;②月销量是 ()件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com