
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4). (Ⅰ)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(Ⅱ)以点O为位似中心,将△ABC缩小为原来的 ![]() ,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.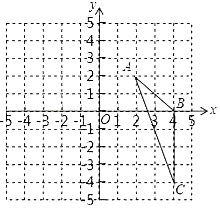
科目:初中数学 来源: 题型:
【题目】甲地与丙地由公路连接,乙地在甲、丙两地之间,一辆汽车在下午1点钟从离甲地10千米的M地出发向乙地匀速前进,15分钟后离甲地20千米,当汽车行驶到离甲地150千米的乙地时,接到通知要在下午5点前赶到离乙地30千米的丙地.汽车若按原速能否按时到达?若能,是在几点几时到达;若不能,车速应提高到多少才能按时到达?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图. 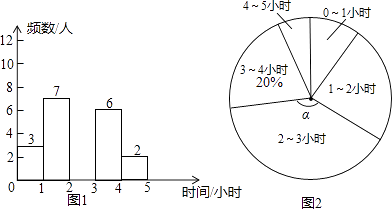
根据上述信息,解答下列问题:
(1)本次抽取的学生人数是;扇形统计图中的圆心角α等于;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求值问题中,我们经常遇到利用整体思想来解决问题.
例如1:已知:x+2y﹣3z=2,2x+y+6z=1,求:x+y+z的值
解:令x+2y﹣3z=2﹣﹣﹣﹣﹣①2x+y+6z=1﹣﹣﹣﹣﹣﹣②
①+②得3x+3y+3z=3所以x+y+z=1
已知![]() 求x+2y的值
求x+2y的值
解:①×2得:2x+2y=﹣10③
②﹣③得:x+2y=11
利用材料中提供的方法,解决下列问题
(1)已知:关于x,y的二元一次方程组![]() 的解满足x﹣y=6,求m的值
的解满足x﹣y=6,求m的值
(2)某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成,乙种盆景由10朵红花和12朵黄花搭配而成,丙咱盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,求黄花一共用了多少朵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,M、N两动点分别从A.C两点同时出发沿正方形的边开始移动,点M按逆时针方向移动,点N按顺时针方向移动,若点M的速度是点N的4倍,则它们第2018次相遇在边_____上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)当∠BAD=60°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y= ![]() x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.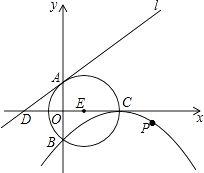
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时.求出点P的坐标及最小距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com