
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
【答案】
(1)解:由题意可知,50次摸球实验活动中,出现红球20次,黄球30次,
∴红球所占百分比为20÷50=40%,
黄球所占百分比为30÷50=60%,
答:红球占40%,黄球占60%
(2)解:由题意可知,50次摸球实验活动中,出现有记号的球4次,
∴总球数为8÷ ![]() =100,
=100,
∴红球数为100×40%=40,
答:盒中红球有40个
【解析】(1)根据表格数据可以得到50次摸球实验活动中,出现红球20次,黄球30次,由此即可求出盒中红球、黄球各占总球数的百分比;(2)由题意可知50次摸球实验活动中,出现有记号的球4次,由此可以求出总球数,然后利用(1)的结论即可求出盒中红球.
【考点精析】解答此题的关键在于理解用频率估计概率的相关知识,掌握在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率.


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象,下列结论错误的是( ) 
A.二次函数y=ax2+bx+c的最大值为4
B.常数项c为3
C.一元二次方程ax2+bx+c=0的两根之和为﹣2
D.使y≤3成立的x的取值范围是x≥0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)当∠BAD=60°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=10,BC=8,P为AD上一点,将△ABP沿BP翻折至△EBP(点A落在点E处),PE与CD相交于点O,且OE=OD,则DP的长为( )

A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.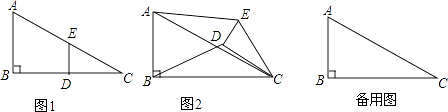
(1)问题发现
①当α=0°时, ![]() =;②当α=180°时,
=;②当α=180°时, ![]() = .
= .
(2)拓展探究
试判断:当0°≤α<360°时, ![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。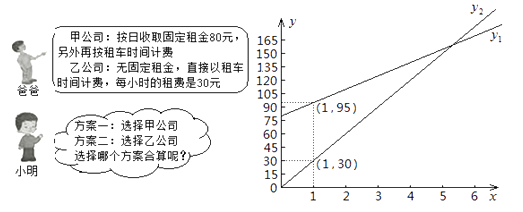
根据以上信息,解答下列问题:
(1)设租车时间为 ![]() 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 ![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 ![]() 元,分别求出
元,分别求出 ![]() ,
, ![]() 关于
关于 ![]() 的函数表达式;
的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com