
【题目】如图是二次函数y=ax2+bx+c的图象,下列结论错误的是( ) 
A.二次函数y=ax2+bx+c的最大值为4
B.常数项c为3
C.一元二次方程ax2+bx+c=0的两根之和为﹣2
D.使y≤3成立的x的取值范围是x≥0
【答案】D
【解析】解:A、观察图象知最高点为(﹣1,4),故最大值为4正确,不符合题意; B、与y轴的交点为(0,3),故常数项为3,正确,不符合题意;
C、一元二次方程ax2+bx+c=0的两根之和为﹣3+1=﹣2,正确,不符合题意;
D、使y≤3成立的x的取值范围是x≤﹣2或y≥0,故错误,符合题意;
故选D.
【考点精析】掌握二次函数的性质和二次函数的最值是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.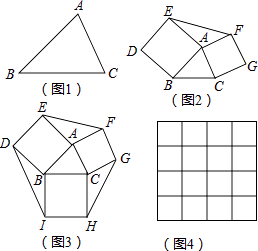
(1)图1中的△ABC的BC边上有一点D,线段AD将△ABC分成两个互补三角形,则点D在BC边的处.
(2)证明:图2中的△ABC分割成两个互补三角形面积相等;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI,已知三个正方形面积分别是17、13、10.则图3中六边形DEFGHI的面积为 . (提示:可先利用图4求出△ABC的面积)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A( ![]() ,0),B(3
,0),B(3 ![]() ,2),C(0,2).动点D以每秒1个单位的速度从点O出发沿OC向终点C运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动.过点E作EF⊥AB,交BC于点F,连接DA、DF.设运动时间为t秒.
,2),C(0,2).动点D以每秒1个单位的速度从点O出发沿OC向终点C运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动.过点E作EF⊥AB,交BC于点F,连接DA、DF.设运动时间为t秒.
(1)求∠ABC的度数;
(2)当t为何值时,AB∥DF;
(3)设四边形AEFD的面积为S.①求S关于t的函数关系式;
②若一抛物线y=﹣x2+mx经过动点E,当S<2 ![]() 时,求m的取值范围(写出答案即可).
时,求m的取值范围(写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,
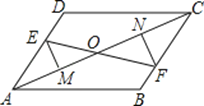
求证:(1)EM=FN;
(2)EF与MN互相平分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图甲是任意一个直角三角形ABC,它的两条直角边的长分别为a,b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.
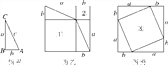
(1)图乙、图丙中①②③都是正方形.由图可知:①是以________为边长的正方形,②是以________为边长的正方形,③是以________为边长的正方形;
(2)图乙中①的面积为________,②的面积为________,图丙中③的面积为________;
(3)图乙中①②面积之和为__________;
(4)图乙中①②的面积之和与图丙中正方形③的面积有什么关系?为什么?由此你能得到关于直角三角形三边长的关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com