
分析 (1)分别根据特殊角的三角函数值、0指数幂、负整数指数幂、二次根式的运算法则计算出各数,再根据实数的运算法则进行计算即可;
(2)先把常数项移到等号的右边,再在等式的两边同时加上一次项系数一半的平方,配成完全平方式,然后开方即可得出答案.
解答 解:(1)$\sqrt{12}$+(π-2016)0+($\frac{1}{3}$)-1-6tan30°
=2$\sqrt{3}$+1+3-6×$\frac{\sqrt{3}}{3}$
=2$\sqrt{3}$+1+3-2$\sqrt{3}$
=4;
(2)x2-6x-4=0,
x2-6x=4,
x2-6x+9=13,
(x-3)2=13,
x-3=±$\sqrt{13}$,
x1=3+$\sqrt{13}$,x2=3-$\sqrt{13}$.
点评 此题考查了特殊角的三角函数值、0指数幂、负整数指数幂、二次根式的运算法则和配方法解一元二次方程的步骤,熟记以上知识是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
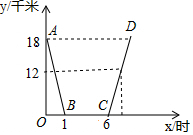 10月2日早晨8点,小华和同学骑自行车去净月潭游玩,当天按原路返回,如图,是小华出行的过程中,他距净月潭的距离y(千米)与他离开家的时间x(小时)之间的函数图象.
10月2日早晨8点,小华和同学骑自行车去净月潭游玩,当天按原路返回,如图,是小华出行的过程中,他距净月潭的距离y(千米)与他离开家的时间x(小时)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
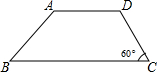 如图,一条公路路基的横断面是梯形(AD∥BC),路基顶宽AD=8米,高3米,斜坡AB的坡度为i=1:1,斜坡DC的坡角∠C=60°.
如图,一条公路路基的横断面是梯形(AD∥BC),路基顶宽AD=8米,高3米,斜坡AB的坡度为i=1:1,斜坡DC的坡角∠C=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D位.测得∠DBO=58°,此时B处距离码头O有多远?
如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D位.测得∠DBO=58°,此时B处距离码头O有多远?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com