
 如图,AB是⊙O的直径,C,D为⊙0上的两点,若∠CDB=30°,则∠ABC的度数为60°,cos∠ABC=$\frac{\sqrt{3}}{2}$.
如图,AB是⊙O的直径,C,D为⊙0上的两点,若∠CDB=30°,则∠ABC的度数为60°,cos∠ABC=$\frac{\sqrt{3}}{2}$. 分析 由于AB是⊙O的直径,由圆周角定理可知∠ACB=90°,则∠A和∠ABC互余,欲求∠ABC需先求出∠A的度数,已知了同弧所对的圆周角∠CDB的度数,则∠A=∠CDB,由此得解.
解答  解:连接AC,
解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,即∠A+∠ABC=90°;
又∵∠A=∠CDB=30°,
∴∠ABC=90°-∠A=60°,
∴cos∠ABC=$\frac{\sqrt{3}}{2}$.
故答案为:60°$\frac{\sqrt{3}}{2}$.
点评 此题主要考查了圆周角定理及其推论,半圆(弧)和直径所对的圆周角是直角,同弧所对的圆周角相等,还考查了三角函数,掌握圆周角定理是解题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
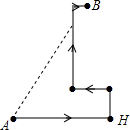 假期中,王强和同学们到某海岛上去玩探宝旅游,按照探宝图(如图),他们在A点登陆后先往东走8$\sqrt{3}$千米到H点,又往北走2$\sqrt{3}$千米,遇到障碍后又往西走了3$\sqrt{3}$千米,再折向北走了6$\sqrt{3}$千米处往东一拐,再走了$\sqrt{3}$千米就找到宝藏埋藏点B,问:他们共走了多少千米?
假期中,王强和同学们到某海岛上去玩探宝旅游,按照探宝图(如图),他们在A点登陆后先往东走8$\sqrt{3}$千米到H点,又往北走2$\sqrt{3}$千米,遇到障碍后又往西走了3$\sqrt{3}$千米,再折向北走了6$\sqrt{3}$千米处往东一拐,再走了$\sqrt{3}$千米就找到宝藏埋藏点B,问:他们共走了多少千米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c | B. | $\frac{1}{c}$ | C. | $\frac{a-b}{a+b}$ | D. | $\frac{a+b}{a-b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
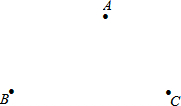 某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com