
分析 (1)设大车租x辆,则小车租(80-x)辆.列出不等式组,求整数解即可解决问题.
(2)设租车费用为w元,则w=1200x+900(80-x)=300x+72000,利用一次函数的增减性,即可解决问题.
解答 解:(1)设大车租x辆,则小车租(80-x)辆.
由题意$\left\{\begin{array}{l}{200x+120(80-x)≥12720}\\{1200x+900(80-x)≤85300}\end{array}\right.$,
解得39≤x≤44$\frac{1}{3}$,
∵x为整数,
∴x=39或40或41或42或43或44.
∴施工方共有6种租车方案.
(2)设租车费用为w元,则w=1200x+900(80-x)=300x+72000,
∵300>0,
∴w随x增大而增大,
∴x=39时,w最小,最小值为83700元.
点评 本题考查一元一次不等式组的应用,一次函数的性质等整数,解题的关键是学会构建不等式组解决实际问题,学会构建一次函数,利用一次函数的性质解决问题,属于中考常考题型.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:选择题
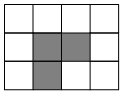 如图,在3×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
如图,在3×4的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:判断题
(本题11分)如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).

(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 累计购物 实际花费 | 500 | 700 | … | x |
| 在甲商场 | 400 | 560 | … | 0.8x |
| 在乙商场 | 410 | 550 | … | 0.7x+60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com