
分析 本题中因为“高BE、CF所在直线交于点O,且点E、F不与点B、C重合”排除了三角形是直角三角形的可能,所以要分两种情况讨论.
解答 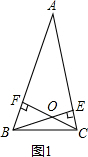 解:本题要分两种情况讨论如图:
解:本题要分两种情况讨论如图:
①当交点在三角形内部时(如1),
在四边形AFOE中,∠AFC=∠AEB=90°,∠A=50°,
根据四边形内角和等于360°得,
∠EOF=180°-∠A=180°-50°=130°.
故∠BOC=130°.
②当交点在三角形外部时(如图2),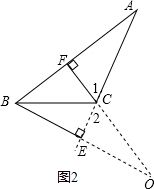 在△AFC中,∠A=50°,∠AFC=90°,
在△AFC中,∠A=50°,∠AFC=90°,
故∠1=180°-90°-50°=40°,
∵∠1=∠2,
∴在△CEO中,∠2=40°,∠CEO=90°,
∴∠EOF=180°-90°-40°=70°,即∠BOC=50°.
点评 本题考查的是三角形内角和定理,在解答此题时要注意进行分类讨论,不要漏解.


科目:初中数学 来源: 题型:选择题
| A. | p>2 | B. | p>0 | C. | p≤2 | D. | 0<p≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
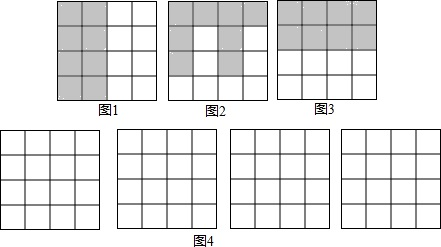
 如图,∠AOB=45°,过OA上到点O的距离分别为1的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3….则第一个黑色梯形的面积S1=4;观察图中的规律,第n(n为正整数)个黑色梯形的面积Sn=8n-4.
如图,∠AOB=45°,过OA上到点O的距离分别为1的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3….则第一个黑色梯形的面积S1=4;观察图中的规律,第n(n为正整数)个黑色梯形的面积Sn=8n-4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )| A. | 34° | B. | 36° | C. | 38° | D. | 40° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com