
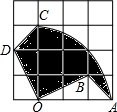
 如图,在4×4的正方形网格中,每个小正方形的边长均为1,将△AOB绕点O逆时针旋转90°得到△COD,则旋转过程中形成的阴影部分的面积为$\frac{9}{4}π$.
如图,在4×4的正方形网格中,每个小正方形的边长均为1,将△AOB绕点O逆时针旋转90°得到△COD,则旋转过程中形成的阴影部分的面积为$\frac{9}{4}π$.  初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
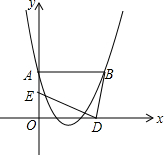 抛物线y=x2+bx+c经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
抛物线y=x2+bx+c经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
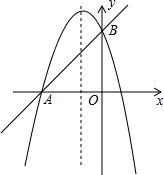 如图,已知抛物线y=-x2+bx+c与直线AB相交于A(-3,0),B(0,3)两点.
如图,已知抛物线y=-x2+bx+c与直线AB相交于A(-3,0),B(0,3)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
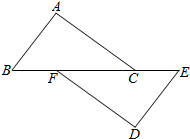 如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是AB=DE(只需写一个,不添加辅助线).
如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是AB=DE(只需写一个,不添加辅助线).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com